题目内容
已知0<b<1+a,记关于x的不等式(x-b)2>(ax)2的解集为M.
(1)若集合M中的整数有无限个,求a的范围;
(2)若集合M中的整数恰有3个,求证:1<a<3.
解:(1)由(x-b)2>(ax)2 得[(1+a)x-b][(1-a)x-b]>0,由于0<b<1+a,
①若1-a=0,即a=1时,不等式化为(2x-b)(-b)>0,
解得M={x|x< },显然M中的整数有无限个,符合条件.
},显然M中的整数有无限个,符合条件.
②1-a≠0,即a≠1时,若要有无数个整数解,则应1-a>0,即a<1;
再由已知条件0<b<1+a,可得a>-1.
综上可知-1<a≤1.
(2)由(1)知1-a<0,即a>1时,x的解在两个实数之间,不等式即(x- )(x-
)(x-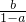 )<0,
)<0,
又可得 ,所以集合M=
,所以集合M= .
.
若要M中的整数恰有3个,则 ,
,
所以, ,解得a<3.
,解得a<3.
综上可知1<a<3.
分析:(1)由题意可得①若1-a=0,M={x|x< },显然M中的整数有无限个,符合条件.②1-a≠0,若要有无数个整数解,则应1-a>0,即a<1,再由已知0<b<1+a,得到a的范围.
},显然M中的整数有无限个,符合条件.②1-a≠0,若要有无数个整数解,则应1-a>0,即a<1,再由已知0<b<1+a,得到a的范围.
(2)由(1)知1-a<0,即a>1时,x的解在两个实数之间,集合M= ,若要M中的整数恰有3个,则
,若要M中的整数恰有3个,则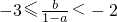 ,从而得到
,从而得到 ,求得a<3,进而得到命题成立.
,求得a<3,进而得到命题成立.
点评:本题主要考查一元二次不等式的应用,体现了分类讨论的数学思想,属于中档题.
①若1-a=0,即a=1时,不等式化为(2x-b)(-b)>0,
解得M={x|x<
 },显然M中的整数有无限个,符合条件.
},显然M中的整数有无限个,符合条件.②1-a≠0,即a≠1时,若要有无数个整数解,则应1-a>0,即a<1;
再由已知条件0<b<1+a,可得a>-1.
综上可知-1<a≤1.
(2)由(1)知1-a<0,即a>1时,x的解在两个实数之间,不等式即(x-
 )(x-
)(x-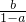 )<0,
)<0,又可得
 ,所以集合M=
,所以集合M= .
.若要M中的整数恰有3个,则
 ,
,所以,
 ,解得a<3.
,解得a<3.综上可知1<a<3.
分析:(1)由题意可得①若1-a=0,M={x|x<
 },显然M中的整数有无限个,符合条件.②1-a≠0,若要有无数个整数解,则应1-a>0,即a<1,再由已知0<b<1+a,得到a的范围.
},显然M中的整数有无限个,符合条件.②1-a≠0,若要有无数个整数解,则应1-a>0,即a<1,再由已知0<b<1+a,得到a的范围.(2)由(1)知1-a<0,即a>1时,x的解在两个实数之间,集合M=
 ,若要M中的整数恰有3个,则
,若要M中的整数恰有3个,则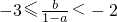 ,从而得到
,从而得到 ,求得a<3,进而得到命题成立.
,求得a<3,进而得到命题成立.点评:本题主要考查一元二次不等式的应用,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目