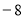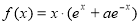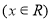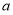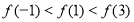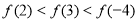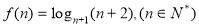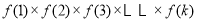题目内容
已知函数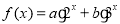 ,其中常数
,其中常数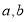 满足
满足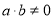
(1)若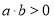 ,判断函数
,判断函数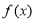 的单调性;
的单调性;
(2)若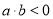 ,求
,求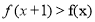 时的
时的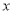 的取值范围.
的取值范围.
(1)Ⅰ当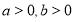 ,
,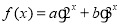 在
在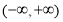 单调递增
单调递增
Ⅱ当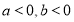 ,
,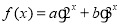 在
在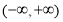 单调递减
单调递减
(2)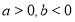 时,
时, ;
;
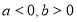 时,
时,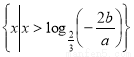
【解析】
试题分析: (1)由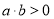 ,说明
,说明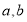 同号,根据指数函数在底数大于1时为增函数可得
同号,根据指数函数在底数大于1时为增函数可得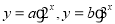 的单调性,然后由在相同区间内增函数的和为增函数,减函数的和为减函数可得函数
的单调性,然后由在相同区间内增函数的和为增函数,减函数的和为减函数可得函数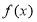 的单调性;
的单调性;
(2)由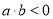 ,说明
,说明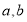 异号,把
异号,把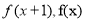 代入不等式
代入不等式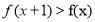 ,整理后由
,整理后由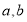 异号,然后分类讨论求解指数不等式即可得到
异号,然后分类讨论求解指数不等式即可得到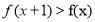 时
时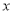 的取值范围.
的取值范围.
试题解析:
(1)由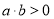 ,则
,则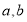 同号
同号
Ⅰ当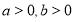 ,则
,则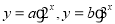 在
在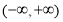 单调递增
单调递增
所以,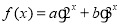 在
在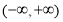 单调递增 2分
单调递增 2分
Ⅱ当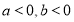 ,则
,则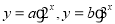 在
在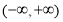 单调递减
单调递减
所以,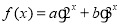 在
在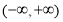 单调递减 4分
单调递减 4分
(2)不等式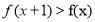 即是:
即是: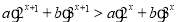
 即
即
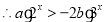 8分
8分
因为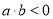 ,则
,则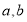 异号
异号
Ⅰ当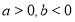 ,则有
,则有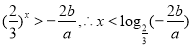 10分
10分
Ⅱ当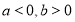 ,则有
,则有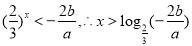 12分
12分
综上,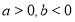 时,
时, 
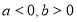 时,
时,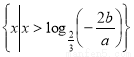 14分
14分
考点:函数单调性得判断,指数不等式得求解方法,分类讨论应用.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目