题目内容
已知 当
当 取得最小值时,直线
取得最小值时,直线 与曲线
与曲线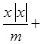
 的交点个数为
的交点个数为
2
解析试题分析:∵
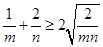 ,
,
∴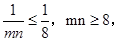 当且仅当
当且仅当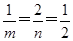 ,即
,即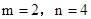 时,
时,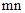 取得最小值8,
取得最小值8,
故曲线方程为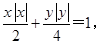
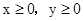 时,方程化为
时,方程化为 ;
;
当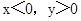 时,方程化为
时,方程化为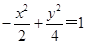 ,
,
当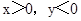 时,方程化为
时,方程化为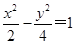 ,
,
当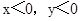 时,无意义,
时,无意义,
由圆锥曲线可作出方程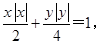 和直线
和直线 与的图象,
与的图象,
由图象可知,交点的个数为2.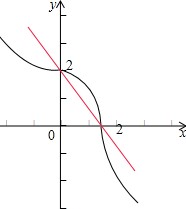
考点:基本不等式,直线与圆锥曲线的位置关系.

练习册系列答案
相关题目
题目内容
已知 当
当 取得最小值时,直线
取得最小值时,直线 与曲线
与曲线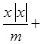
 的交点个数为
的交点个数为
2
解析试题分析:∵
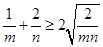 ,
,
∴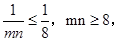 当且仅当
当且仅当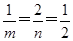 ,即
,即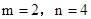 时,
时,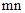 取得最小值8,
取得最小值8,
故曲线方程为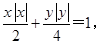
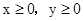 时,方程化为
时,方程化为 ;
;
当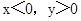 时,方程化为
时,方程化为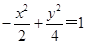 ,
,
当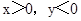 时,方程化为
时,方程化为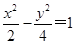 ,
,
当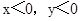 时,无意义,
时,无意义,
由圆锥曲线可作出方程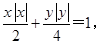 和直线
和直线 与的图象,
与的图象,
由图象可知,交点的个数为2.
考点:基本不等式,直线与圆锥曲线的位置关系.
