题目内容
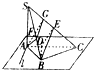 如图,在△ABC中,AB⊥BC,SA⊥平面ABC,DE垂直平分SC,且分别交AC、SC于点D、E,又SA=AB,SB=BC,求二面角E-BD-C的大小.
如图,在△ABC中,AB⊥BC,SA⊥平面ABC,DE垂直平分SC,且分别交AC、SC于点D、E,又SA=AB,SB=BC,求二面角E-BD-C的大小.分析:不妨设AB=
=SA,利用已知和勾股定理可得SB=BC=
,AC.在Rt△SAC中,可得∠SCA,SC.利用DE垂直平分SC,可得EC,DC.利用余弦定理可得BD,再利用勾股定理的逆定理可得BD⊥DC.利用线面、面面垂直的性质定理可得BD⊥平面SAC,因此BD⊥DE.于是得到∠EDC是二面角E-BD-C的平面角.
| 3 |
| 6 |
解答:解:如图所示.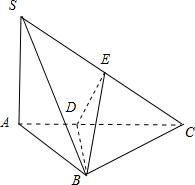
不妨设AB=
=SA,则SB=BC=
.
∵AB⊥BC,∴AC=
=3.
∵SA⊥平面ABC,∴SA⊥AC,∴tan∠SCA=
=
,∴∠SCA=30°.∴SC=2
.
∵DE垂直平分SC,∴EC=
,DC=
=2.
在Rt△ABC中,cos∠BCD=
=
.
在△BCD中,由余弦定理可得:BD2=BC2+DC2-2BC•DC•cos∠BCD=(
)2+22-2×
×2×
=2,
∴DB2+DC2=6=BC2.
∴∠BDC=90°.
∴BD⊥DC.
∵SA⊥平面ABC,∴平面SAC⊥平面ABC.
∴BD⊥平面SAC,∴BD⊥DE.
∴∠EDC是二面角E-BD-C的平面角,且∠EDC=60°.

不妨设AB=
| 3 |
| 6 |
∵AB⊥BC,∴AC=
| AB2+BC2 |
∵SA⊥平面ABC,∴SA⊥AC,∴tan∠SCA=
| SA |
| AC |
| ||
| 3 |
| 3 |
∵DE垂直平分SC,∴EC=
| 3 |
| EC |
| cos30° |
在Rt△ABC中,cos∠BCD=
| BC |
| AC |
| ||
| 3 |
在△BCD中,由余弦定理可得:BD2=BC2+DC2-2BC•DC•cos∠BCD=(
| 6 |
| 6 |
| ||
| 3 |
∴DB2+DC2=6=BC2.
∴∠BDC=90°.
∴BD⊥DC.
∵SA⊥平面ABC,∴平面SAC⊥平面ABC.
∴BD⊥平面SAC,∴BD⊥DE.
∴∠EDC是二面角E-BD-C的平面角,且∠EDC=60°.
点评:熟练掌握线面、面面垂直的性质定理、二面角的平面角的定义、勾股定理及其逆定理、余弦定理垂直平分线的性质等是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,
如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm, 如图,在△ABC中,设
如图,在△ABC中,设 如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3.
如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3. 如图,在△ABC中,已知
如图,在△ABC中,已知