题目内容
【题目】学号为1,2,3的三位小学生,在课余时间一起玩“掷骰子爬楼梯”游戏,规则如下:投掷一颗骰子,将每次出现点数除以3,若学号与之同余(同除以3余数相同),则该小学生可以上2阶楼梯,另外两位只能上1阶楼梯,假定他们都是从平地(0阶楼梯)开始向上爬,且楼梯数足够多.
(1)经过2次投掷骰子后,学号为1的同学站在第X阶楼梯上,试求X的分布列;
(2)经过多次投掷后,学号为3的小学生能站在第n阶楼梯的概率记为![]() ,试求
,试求![]() ,
,![]() ,
,![]() 的值,并探究数列
的值,并探究数列![]() 可能满足的一个递推关系和通项公式.
可能满足的一个递推关系和通项公式.
【答案】(1)答案见解析.(2)![]() ,
,![]() ,
,![]() ,
,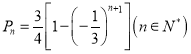
【解析】
(1)由题意学号为1的同学可以上2阶楼梯的概率为![]() ,可以上1阶楼梯的概率为
,可以上1阶楼梯的概率为![]() ,分别求出
,分别求出![]() 、
、![]() 、
、![]() ,即可得解;
,即可得解;
(2)由题意可得![]() 、
、![]() 、
、![]() ;由题意
;由题意![]() 且
且![]() ,构造新数列即可得数列
,构造新数列即可得数列![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列,再利用累加法即可得解.
为公比的等比数列,再利用累加法即可得解.
(1)由题意,当投掷骰子出现1、4时,学号为1的同学可以上2阶楼梯,概率为![]() ,
,
当投掷骰子出现其他点数时,学号为1的同学可以上1阶楼梯,概率为![]() ,
,
由题意![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
所以X的分布列为:
X | 2 | 3 | 4 |
P |
|
|
|
(2)![]() 表示学号为3的小朋友能站在第1阶楼梯的概率,
表示学号为3的小朋友能站在第1阶楼梯的概率,
根据投掷骰子的规则,若出现点数为3或6,则他直接站在第2阶楼梯,否则站在第1阶楼梯.
故![]() ,同理可得:
,同理可得:
![]() ,
,![]() ,
,
由于学号为3的小朋友能够站在第n阶楼梯,有两种可能:
从第![]() 阶楼梯投掷点数为3或6直接登2个台阶上来,
阶楼梯投掷点数为3或6直接登2个台阶上来,
或从第![]() 阶楼梯只登1个台阶上来.
阶楼梯只登1个台阶上来.
根据骰子投掷规则,登两阶的概率是![]() ,登一阶的概率是
,登一阶的概率是![]() ,
,
故![]() 且
且![]() (*)
(*)
将(*)式可变形为![]() ,
,
从而知:数列![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列,
为公比的等比数列,
则有![]() .
.
进而可得:当![]() 时,
时,![]()
![]()
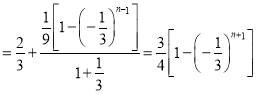 ;
;
当![]() 时,
时, ;
;
所以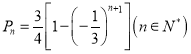 .
.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目