题目内容
若在⊿ABC中,满足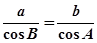 ,则三角形的形状是
,则三角形的形状是
A等腰或直角三角形 B 等腰三角形 C直角三角形 D不能判定
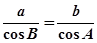 ,则三角形的形状是
,则三角形的形状是A等腰或直角三角形 B 等腰三角形 C直角三角形 D不能判定
A
分析:由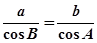 ,结合正弦定理可得,
,结合正弦定理可得, ,则有sin2A=sin2B,从而可判断形状
,则有sin2A=sin2B,从而可判断形状
解答:因为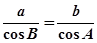 ,由正弦定理可得,
,由正弦定理可得,
∴sinAcosA=sinBcosB,即sin2A=sin2B
∴2A=2B或2A+2B=π
∴A=B或A+B=
故选A
点评:本题主要考查了三角形的正弦定理二倍角公式的应用,解答本题容易漏掉2A+2B=π的情况.
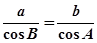 ,结合正弦定理可得,
,结合正弦定理可得, ,则有sin2A=sin2B,从而可判断形状
,则有sin2A=sin2B,从而可判断形状解答:因为
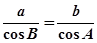 ,由正弦定理可得,
,由正弦定理可得,
∴sinAcosA=sinBcosB,即sin2A=sin2B
∴2A=2B或2A+2B=π
∴A=B或A+B=

故选A
点评:本题主要考查了三角形的正弦定理二倍角公式的应用,解答本题容易漏掉2A+2B=π的情况.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
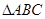 中,
中,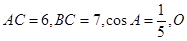 是
是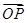 =
=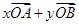 ,其中
,其中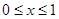 ,
,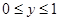 ,动点
,动点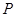
 的轨迹所覆盖的面积为
的轨迹所覆盖的面积为




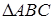 中,角
中,角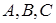 所对的边
所对的边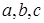 ,已知
,已知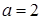 ,
,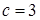 ,
,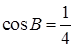 ;(1)求边
;(1)求边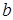 的值;(2)求
的值;(2)求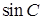 的值。
的值。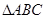 中,
中,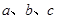 分别为内角
分别为内角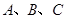 的对边,且
的对边,且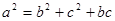
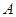 的大小;
的大小;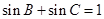 ,试求内角B、C的大小.
,试求内角B、C的大小.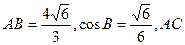 边上的中线BD=
边上的中线BD=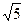 ,
,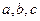 ,若
,若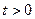 ,则边长是
,则边长是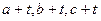 的三角形的形状是
的三角形的形状是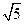 ,b=
,b=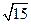 ,A=300,则边c= 。
,A=300,则边c= 。