题目内容
如图，已知直角梯形ABCD的上底BC＝
，BC∥AD，BC＝
AD，CD⊥AD，平面PDC⊥平面ABCD，△PCD是边长为2的等边三角形.
(1)证明：AB⊥PB；
(2)求三棱锥A－PBD的体积.
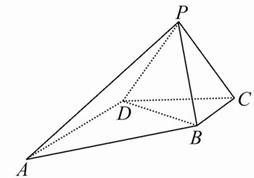
(1)在直角梯形ABCD中，
因为AD＝2，BC＝，CD＝2，
所以AB＝
＝
.
因为BC⊥CD，平面PDC⊥平面ABCD，平面PDC∩平面ABCD＝CD，所以BC⊥平面PDC，因此在Rt△BCP中，PB＝
＝.
因为BC∥AD所以AD⊥平面PDC，
所以在Rt△PAD中，
PA＝
＝
＝2
.
所以在△PAB中，PA2＝AB2＋PB2，所以AB⊥PB.
(2)过P作PE⊥DC，△PCD为等边三角形，
∴E为DC中点，易得PE⊥平面ABCD，
且PE＝，所以VA－PBD＝VP－ABD＝
S△ABD·PE
＝×(·AD·DC)·
＝
×2×2×＝
.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，已知四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥DC，∠ABC=45°，DC=1，AB=2，PA⊥平面ABCD，PA=1．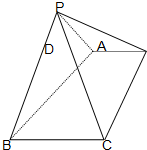
如图：已知四棱锥P-ABCD的底面为直角梯形，AD∥BC，∠BCD=90，PA=PB，PC=PD．
如图，已知直角梯形ABCD的上底BC=