题目内容
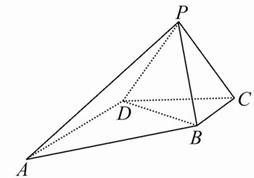
如图,已知直角梯形ABCD中,AB⊥BC,AB=AD=a,BC=3a,E是BC边上一动点,以DE为棱把△CDE折起,使其成直二面角C-DE-A,求四棱锥C-ABED体积的最大值.
答案:
解析:
解析:
|
解:设∠DEC=θ,作CF⊥DE于F,DH⊥BC于H,则EH=acotθ,CF=CEsinθ=(2a+acotθ)·sinθ, ∴ |

练习册系列答案
相关题目

 -
- (1-
(1- ·sinθ(4-
·sinθ(4- (5sinθ-
(5sinθ- ).当E与B点重合时,θ有最小值:
).当E与B点重合时,θ有最小值: =
= ;当E→C点时,θ→π-
;当E→C点时,θ→π- ,π-
,π- ).当
).当 时,5sinθ-
时,5sinθ- 是增函数,当θ∈[
是增函数,当θ∈[ ,π-
,π- 如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.
如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.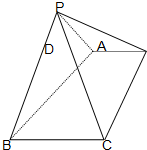 如图:已知四棱锥P-ABCD的底面为直角梯形,AD∥BC,∠BCD=90,PA=PB,PC=PD.
如图:已知四棱锥P-ABCD的底面为直角梯形,AD∥BC,∠BCD=90,PA=PB,PC=PD. 如图,已知直角梯形ABCD的上底BC=
如图,已知直角梯形ABCD的上底BC=