题目内容
在平面直角坐标系中,点A(1,2),B(7,10)到直线l 距离分别为2和6,则满足条件的直线条数是( )
| A、1 | B、2 | C、3 | D、4 |
分析:以A为圆心,2为半径画出圆A,以B为圆心,6为半径画出圆B,然后利用两点间的距离求出两圆心间的距离d,根据两半径相加小于d得两圆位置关系是相离,即为得到两圆的公切线有4条,则满足题意的直线有4条.
解答:解:根据题意画出图形,如图所示:
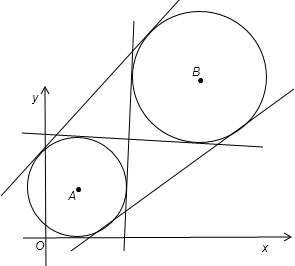
以点A为圆心,2为半径画出圆A,以点B为圆心,6为半径画出圆B,
∵圆心距d=|AB|=
=10,圆A半径r=2,圆B半径R=6,
∴d>R+r,即圆A与圆B相离,故存在4条公切线,
则满足题意的直线有4条.
故选D

以点A为圆心,2为半径画出圆A,以点B为圆心,6为半径画出圆B,
∵圆心距d=|AB|=
| (7-1)2+(10-2)2 |
∴d>R+r,即圆A与圆B相离,故存在4条公切线,
则满足题意的直线有4条.
故选D
点评:此题考查了两圆位置关系的判别方法,以及数形结合数学思想的运用.把原题的问题转化为两圆公切线的问题是解本题的关键.
圆与圆位置关系的判别方法是:(d表示两圆心间的距离,R,r表示两圆的半径),
(1)0≤d<R-r,两圆内含;
(2)d=R-r,两圆内切;
(3)R-r<d<R+r,两圆相交;
(4)d=R+r,两圆外切;
(5)d>R+r,两圆相离.
圆与圆位置关系的判别方法是:(d表示两圆心间的距离,R,r表示两圆的半径),
(1)0≤d<R-r,两圆内含;
(2)d=R-r,两圆内切;
(3)R-r<d<R+r,两圆相交;
(4)d=R+r,两圆外切;
(5)d>R+r,两圆相离.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目