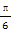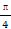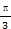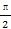题目内容
在正三棱柱ABC—A1B1C1中,D是AC的中点,AB1⊥BC1,则平面DBC1与平面CBC1所成的角为( )
| A.30° | B.45° | C.60° | D.90° |
B
解析

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
在空间直角坐标系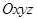 中,已知
中,已知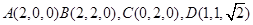 .若
.若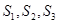 分别是三棱锥
分别是三棱锥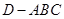 在
在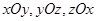 坐标平面上的正投影图形的面积,则( )
坐标平面上的正投影图形的面积,则( )
A.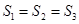 | B.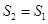 且 且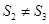 |
C.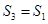 且 且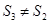 | D.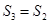 且 且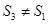 |
已知正四棱柱 中
中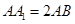 ,则
,则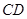 与平面
与平面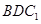 所成角的正弦值等于( )
所成角的正弦值等于( )
A.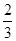 | B.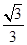 | C.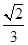 | D.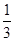 |
向量 =(2,4,x),
=(2,4,x),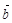 =(2,y,2),若|
=(2,y,2),若| |=6,且
|=6,且 ⊥
⊥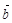 ,则x+y的值为( )
,则x+y的值为( )
| A.-3 | B.1 | C.-3或1 | D.3或1 |
若三点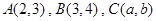 共线,则有( )
共线,则有( )
A.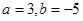 | B.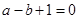 | C.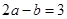 | D.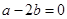 |
△ABC的顶点分别为A(1,-1,2),B(5,-6,2),C(1,3,-1)则AC边上的高BD等于( )
| A.2 |
B.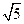 |
| C.5 |
| D.6 |
如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F且EF=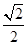 ,则下列结论中错误的是 ( ).
,则下列结论中错误的是 ( ).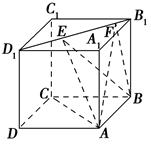
| A.AC⊥BE |
| B.EF∥平面ABCD |
| C.三棱锥A-BEF的体积为定值 |
| D.异面直线AE,BF所成的角为定值 |
 中,
中, ,
,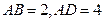 将
将 沿
沿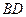 折起到
折起到 的位置,使平面
的位置,使平面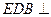 平面
平面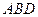
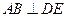 (Ⅱ)求三棱锥
(Ⅱ)求三棱锥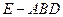 的侧面积。
的侧面积。