题目内容
设两个非零向量 和
和 不共线.
不共线.(1)如果
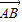 =
= +
+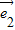 ,
,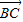 =
=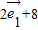
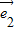 ,
,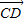 =
=
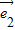 ,求证:A、B、D三点共线;
,求证:A、B、D三点共线;(2)若
 =2,
=2,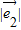 =3,
=3,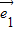 与
与 的夹角为60°,是否存在实数m,使得m
的夹角为60°,是否存在实数m,使得m
 与
与
 垂直?
垂直?
【答案】分析:(1)要证A、B、D三点共线,只需证明 =
= 即可.
即可.
(2)要使m
 与
与
 垂直,,则(m
垂直,,则(m
 )•(
)•(
 )=0,展开求出m的值即可.
)=0,展开求出m的值即可.
解答:证明:(1)∵ =
= +
+ +
+ =(
=( +
+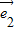 )+(
)+(
 )+(
)+(
 )=6(
)=6( +
+ )=6
)=6
∴
 且
且 与
与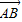 有共同起点,∴A、B、D三点共线
有共同起点,∴A、B、D三点共线
(2)假设存在实数m,使得m
 与
与
 垂直,则(m
垂直,则(m
 )•(
)•(
 )=0
)=0
∴ ,
,
∵ =2,
=2, =3,
=3, 与
与 的夹角为60°
的夹角为60°
∴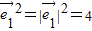 ,
, ,
,
∴4m+3(1-m)-9=0,
∴m=6,故存在实数m=6,使得m
 与
与
 垂直.
垂直.
点评:本题考查了平面向量的共线与垂直,属于基础题型.
 =
= 即可.
即可.(2)要使m

 与
与
 垂直,,则(m
垂直,,则(m
 )•(
)•(
 )=0,展开求出m的值即可.
)=0,展开求出m的值即可.解答:证明:(1)∵
 =
= +
+ +
+ =(
=( +
+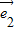 )+(
)+(
 )+(
)+(
 )=6(
)=6( +
+ )=6
)=6
∴

 且
且 与
与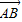 有共同起点,∴A、B、D三点共线
有共同起点,∴A、B、D三点共线(2)假设存在实数m,使得m

 与
与
 垂直,则(m
垂直,则(m
 )•(
)•(
 )=0
)=0∴
 ,
,∵
 =2,
=2, =3,
=3, 与
与 的夹角为60°
的夹角为60°∴
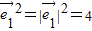 ,
, ,
,
∴4m+3(1-m)-9=0,
∴m=6,故存在实数m=6,使得m

 与
与
 垂直.
垂直.点评:本题考查了平面向量的共线与垂直,属于基础题型.

练习册系列答案
相关题目
 和
和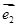 不共线;
不共线; ,使
,使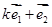 和
和 共线;
共线;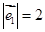 ,
,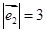 ,
,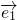 和
和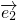 不共线.
不共线.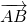 =
=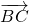 =
=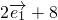
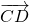 =
=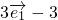
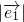 =2,
=2,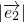 =3,
=3,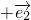 与
与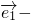
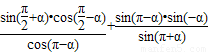 ;
; 和
和 不共线,且
不共线,且 ,
, ,
, ,求证:A,B,D三点在同一直线上.
,求证:A,B,D三点在同一直线上.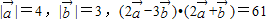 ,求
,求 的值;
的值; 和
和 不共线.如果
不共线.如果 =
=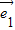 +
+ ,
,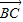 =
=
 ,
, =
=
 ,
,