题目内容
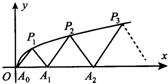 如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).则a1=
如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).则a1=分析:由题意可知直线A0P1为y=
x,然后与y2=3x联立可得到P1的坐标,再由△A0A1P1是正三角形可得到A1的坐标得到a1的值,先根据题意可得到关系,然后根据yn2=3xn得(an-an-1)2=2(an-1+an),从而可猜想数列通项公式an=n(n+1).
| 3 |
解答:解:y=
x ①
y2=3x ②
∴P1(1,
)
∴a1=2,
依题意,得 xn=
,yn=
•
,
由此及yn2=3xn得 (
•
)2=
(an-1+an),
即(an-an-1)2=2(an-1+an).
由(1)可猜想:an=n(n+1)n∈N*
故答案为:2;an=n(n+1)(n∈N*)
| 3 |
y2=3x ②
∴P1(1,
| 3 |
∴a1=2,
依题意,得 xn=
| an-1+an |
| 2 |
| 3 |
| an-an-1 |
| 2 |
由此及yn2=3xn得 (
| 3 |
| an-an-1 |
| 2 |
| 3 |
| 2 |
即(an-an-1)2=2(an-1+an).
由(1)可猜想:an=n(n+1)n∈N*
故答案为:2;an=n(n+1)(n∈N*)
点评:本题考查数列与解析几何的综合题目,解题过程中,用到方程的求解,注意题目中的运算比较繁琐,不要在这种环节出错.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
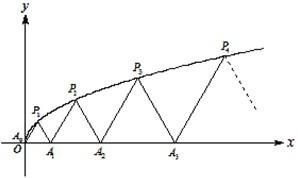 如图,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).
如图,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).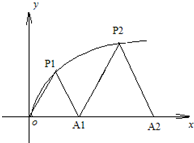 如图,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn) 是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).
如图,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn) 是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点). (2012•闸北区二模)如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…是曲线
(2012•闸北区二模)如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…是曲线