题目内容
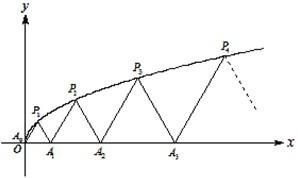 如图,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).
如图,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).(1)写出a1,a2,a3;
(2)求出点An(an,0)(n∈N*)的横坐标an关于n的表达式;并用数学归纳法证明.
分析:(1)由题意可知直线A0P1为y=
x,然后与y2=3x联立可得到P1的坐标,再由△A0A1P1是正三角形可得到A1的坐标得到a1的值,同理可得到a2、a3.
(2)先根据题意可得到关系 xn=
,yn=
•
,然后根据yn2=3xn得(an-an-1)2=2(an-1+an),从而可猜想数列通项公式an=n(n+1),再由数学归纳法证明即可.
| 3 |
(2)先根据题意可得到关系 xn=
| an-1+an |
| 2 |
| 3 |
| an-an-1 |
| 2 |
解答:解(1)a1=2,a2=6,a3=12;
(2)依题意,得 xn=
,yn=
•
,由此及yn2=3xn得 (
•
)2=
(an-1+an),即(an-an-1)2=2(an-1+an).
由(1)可猜想:an=n(n+1)n∈N*
下面用数学归纳法予以证明:
(1)当n=1时,命题显然成立;
(2)假定当n=k时命题成立,即有an=k(k+1),则当n=k+1时,由归纳假设及(ak+1-ak)2=2(ak+ak+1)得[ak+1-k(k+1)]2=2[k(k+1)+ak+1],即(ak+1)2-2(k2+k+1)ak+1+[k(k-1)]•[(k+1)(k+2)]=0,
解之得ak+1=(k+1)(k+2),(ak+1=k(k-1)<ak不合题意,舍去),
即当n=k+1时,命题成立.
由(1)、(2)知:命题成立.
(2)依题意,得 xn=
| an-1+an |
| 2 |
| 3 |
| an-an-1 |
| 2 |
| 3 |
| an-an-1 |
| 2 |
| 3 |
| 2 |
由(1)可猜想:an=n(n+1)n∈N*
下面用数学归纳法予以证明:
(1)当n=1时,命题显然成立;
(2)假定当n=k时命题成立,即有an=k(k+1),则当n=k+1时,由归纳假设及(ak+1-ak)2=2(ak+ak+1)得[ak+1-k(k+1)]2=2[k(k+1)+ak+1],即(ak+1)2-2(k2+k+1)ak+1+[k(k-1)]•[(k+1)(k+2)]=0,
解之得ak+1=(k+1)(k+2),(ak+1=k(k-1)<ak不合题意,舍去),
即当n=k+1时,命题成立.
由(1)、(2)知:命题成立.
点评:本题主要考查求数列通项公式、数列的单调性问题以及二次函数的恒成立问题,考查综合运用能力.

练习册系列答案
相关题目
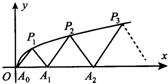 如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).则a1=
如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).则a1=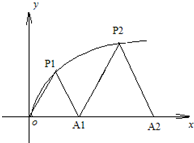 如图,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn) 是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).
如图,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn) 是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点). (2012•闸北区二模)如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…是曲线
(2012•闸北区二模)如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…是曲线