��Ŀ����
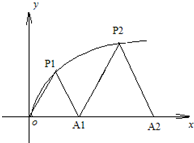 ��ͼ��P1��x1��y1����P2��x2��y2��������Pn��xn��yn����0��y1��y2������yn�� ������C��y2=3x��y��0���ϵ�n���㣬��Ai��ai��0����i=1��2��3����n����x����������ϣ��ҡ�Ai-1AiPi���������Σ�A0������ԭ�㣩��
��ͼ��P1��x1��y1����P2��x2��y2��������Pn��xn��yn����0��y1��y2������yn�� ������C��y2=3x��y��0���ϵ�n���㣬��Ai��ai��0����i=1��2��3����n����x����������ϣ��ҡ�Ai-1AiPi���������Σ�A0������ԭ�㣩����1����a1��a2��a3��ֵ��
��2�������An��an��0����n��N+���ĺ�����an�͵�An-1��an-1��0����n��0��n��N+��������an-1�Ĺ�ϵʽ��
��3�����ݣ�1���Ľ��۲���an����n�ı���ʽ��������ѧ���ɷ�֤����
��������1��������֪����ֱ����a1��a2��a3��ֵ��
��2���루1���������ֱ�ߵķ��̣�ͨ�������An��an��0����n��N+���ĺ�����an���An-1��an-1��0����n��0��n��N+��������an-1���ɵõ�(an-an-1)2=2(an-1+an)��
��3�����ݣ�1���Ľ��۲���an����n�ı���ʽ��ֱ��������ѧ���ɷ�֤������֤�����ɣ�
��2���루1���������ֱ�ߵķ��̣�ͨ�������An��an��0����n��N+���ĺ�����an���An-1��an-1��0����n��0��n��N+��������an-1���ɵõ�(an-an-1)2=2(an-1+an)��
��3�����ݣ�1���Ľ��۲���an����n�ı���ʽ��ֱ��������ѧ���ɷ�֤������֤�����ɣ�
���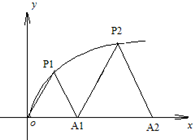 �⣺��1�������⣬OP1ֱ�߷���Ϊy=
�⣺��1�������⣬OP1ֱ�߷���Ϊy=
x�����߷���y2=3x����
���P1��ĺ�����Ϊx1=1�����е����깫ʽ��a1=2 ����2�֣�
ͬ����A1P2ֱ�߷���Ϊy=
��x-2������y2=3x���x2=4 ����3�֣�
�����е����깫ʽ��a2=6��
A2P2ֱ�߷���Ϊy=
��x-6������y2=3x���x3=9
�����е����깫ʽ��a3=12������4�֣�
��2�������⣬��xn=
�١���5�֣�
ֱ��An-1Pn�ķ���Ϊy=
��x-an-1��
Pn��xn��yn���������㷽�̣�����yn=
��xn-an-1���ڡ���6�֣�
�Ѣٴ����ʽ�� yn=
��
-an-1��=
•
�ۣ�7�֣�
��Ϊyn2=3xn �ܡ���8�֣�
�Ѣ�ʽ����ܵ�
(
•
)2=
(an+an-1)��
��(an-an-1)2=2(an-1+an)����9�֣�
��3���ɣ��ɲ��룺an=n��n+1����n��N+���� ��10�֣�
��������ѧ���ɷ�����֤����
��1����n=1ʱ��������Ȼ������
��2���ٶ���n=kʱ�������������ak=k��k+1��������11�֣�
��n=k+1ʱ���ɹ��ɼ��輰
(ak+1-ak)2=2(ak+ak+1)��[ak+1-k(k+1)]2=2[k(k+1)]+ak+1����
��ak+1��2-2��k2+k+1��ak+1+[k��k+1��]•[��k+1����k+2��]=0��
��֮�ã�ak+1=��k+1����k+2������ak+1=k��k-1�����������⣬��ȥ����
����n=k+1ʱ����������� ����13�֣�
�ɣ�1������2��֪����������� ����14�֣�
 �⣺��1�������⣬OP1ֱ�߷���Ϊy=
�⣺��1�������⣬OP1ֱ�߷���Ϊy=| 3 |
���P1��ĺ�����Ϊx1=1�����е����깫ʽ��a1=2 ����2�֣�
ͬ����A1P2ֱ�߷���Ϊy=
| 3 |
�����е����깫ʽ��a2=6��
A2P2ֱ�߷���Ϊy=
| 3 |
�����е����깫ʽ��a3=12������4�֣�
��2�������⣬��xn=
| an-1+an |
| 2 |
ֱ��An-1Pn�ķ���Ϊy=
| 3 |
Pn��xn��yn���������㷽�̣�����yn=
| 3 |
�Ѣٴ����ʽ�� yn=
| 3 |
| an-1+an |
| 2 |
| 3 |
| an-an-1 |
| 2 |
��Ϊyn2=3xn �ܡ���8�֣�
�Ѣ�ʽ����ܵ�
(
| 3 |
| an-an-1 |
| 2 |
| 3 |
| 2 |
��(an-an-1)2=2(an-1+an)����9�֣�
��3���ɣ��ɲ��룺an=n��n+1����n��N+���� ��10�֣�
��������ѧ���ɷ�����֤����
��1����n=1ʱ��������Ȼ������
��2���ٶ���n=kʱ�������������ak=k��k+1��������11�֣�
��n=k+1ʱ���ɹ��ɼ��輰
(ak+1-ak)2=2(ak+ak+1)��[ak+1-k(k+1)]2=2[k(k+1)]+ak+1����
��ak+1��2-2��k2+k+1��ak+1+[k��k+1��]•[��k+1����k+2��]=0��
��֮�ã�ak+1=��k+1����k+2������ak+1=k��k-1�����������⣬��ȥ����
����n=k+1ʱ����������� ����13�֣�
�ɣ�1������2��֪����������� ����14�֣�
���������⿼������������������ϵ����⣬ֱ���������ߵ�λ�ù�ϵ�����еĺ�������������ѧ���ɷ���Ӧ�ã����������������Լ�����������

��ϰ��ϵ�д�
 Сѧ���AB��ϵ�д�
Сѧ���AB��ϵ�д� ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�
�����Ŀ
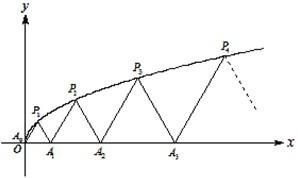 ��ͼ��P1��x1��y1����P2��x2��y2��������Pn��xn��yn����0��y1��y2������yn��������C��y2=3x��y��0���ϵ�n���㣬��Ai��ai��0����i=1��2��3������n����x����������ϣ��ҡ�Ai-1AiPi���������Σ�A0������ԭ�㣩��
��ͼ��P1��x1��y1����P2��x2��y2��������Pn��xn��yn����0��y1��y2������yn��������C��y2=3x��y��0���ϵ�n���㣬��Ai��ai��0����i=1��2��3������n����x����������ϣ��ҡ�Ai-1AiPi���������Σ�A0������ԭ�㣩��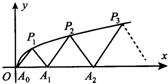 ��ͼ��P1��x1��y1����P2��x2��y2��������Pn��xn��yn����0��y1��y2������yn��������C��y2=3x��y��0���ϵ�n���㣬��Ai��ai��0����i=1��2��3������n����x����������ϣ��ҡ�Ai-1AiPi���������Σ�A0������ԭ�㣩����a1=
��ͼ��P1��x1��y1����P2��x2��y2��������Pn��xn��yn����0��y1��y2������yn��������C��y2=3x��y��0���ϵ�n���㣬��Ai��ai��0����i=1��2��3������n����x����������ϣ��ҡ�Ai-1AiPi���������Σ�A0������ԭ�㣩����a1= ��2012•բ������ģ����ͼ��P1��x1��y1����P2��x2��y2��������Pn��xn��yn������������
��2012•բ������ģ����ͼ��P1��x1��y1����P2��x2��y2��������Pn��xn��yn������������