题目内容
| |||||||||||||||
解析:
(1) |
解:∵f(x)在[-1,0]上是减函数,在[0,2]上是增函数 ∴x=0点是f(x)的一个极值点 ∴ 即x=0是3ax2+2x+c=0的一个根 ∴c=0 分析:(1)由f(x)在[-1,0]上递减,在[0,2]上递增,可得x=0是f(x)的一个极值点,便可求出c的值. |
(2) |
解:∵f(x)在[-1,0]上是减函数,在[0,2]上是增函数, ∴x=0点是f(x)的一个极值点, ∴ 即x=0是3ax2+2x+c=0的一个根. ∴c=0. ∵函数f(x)的图象过点(2,0),∴f(2)=0. ∴8a+4+d=0,即d=-8a-4. 令 ∴x1=0,x2=- ∵f(x)在[0,2]上为增函数,在[4,5]上为减函数,∴x2∈[2,4], 即 ∴-6≤ 即- ∴- 即- 分析:由f(x)在[0,2]上递增,在[4,5]上递减,可得函数的另一个极值点在[2,4]上,这样就可建立相应的不等式求出d的取值范围. |
(3) |
解:假设存在点M(x0,y0),使得曲线y=f(x)在点M处的切线的斜率为3,则 即3a ∴3a 又- ∴△=4+36a<0. ∴不存在点M(x0,y0),使得曲线y=(x)在点M处的切线的斜率为3. 分析:求得f(x)在x=x0时的导数,并使其为3,这样可以建立关于x0的方程,通过判别式判断有无实根就可以确定点M是否存在. |

 阅读快车系列答案
阅读快车系列答案 ≥2,
≥2,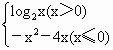 ,则此函数的“友好点对”有
,则此函数的“友好点对”有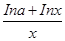 在[1,+∞)上为减函数,求实数a的取值范围.
在[1,+∞)上为减函数,求实数a的取值范围.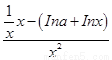 =
=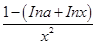 ,因为 f(x)在[1,+∞)上为减函数,故 f ′(x)≤0在[1,+∞)上恒成立,即lna≥1-lnx在[1,+∞)上恒成立.设φ(x)=1-lnx,φ(x)max=1,故lna≥1,a≥e,
,因为 f(x)在[1,+∞)上为减函数,故 f ′(x)≤0在[1,+∞)上恒成立,即lna≥1-lnx在[1,+∞)上恒成立.设φ(x)=1-lnx,φ(x)max=1,故lna≥1,a≥e,