题目内容
已知函数，f(x)＝
－1og2
，求函数f(x)的定义域，并讨论它的奇偶性和单调性．
答案：
提示：
提示：
| 命题意图：本题主要考查函数、对数函数的性质等基本知识，考查逻辑思维能力和分析问题、解决问题的能力．
解题思路：用f(x)中代数式的意义确定函数的定义域，然后用奇偶性和单调性的定义判断函数的奇偶性和单调性． 因为x需满足 所以函数的定义域为(－1，0)U(0，1)． 又∵f(－x)＝－ ∴f(x)是奇函数． 在区间(0，1)内，任取x1、x2∈(0，1)，且设x1<x2，则 f(x1)－f(x2)＝ 由 由于f(x)是奇函数，所以f(x)在(－1，0)内单调递减． 评点：本题在判断单调性的过程中，应用了－个重要的结论，即奇函数在对称区间上的单调性相同．
|
解之，得－1<x<1
－1og2
＝－(
－1og2
)＝－f(x)，
－1og2
－
＋1og2
＝(
－
)＋[1og2
．
－
>０，1og2(
－1)－1og2(
－1)>0，得f(x1)－f(x2)>0，即f(x)在(0，1)内单调递减．
练习册系列答案
相关题目
的事件为A，则事件A发生的概率为
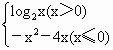，则此函数的“友好点对”有
若
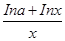在[1，＋∞)上为减函数，求实数a的取值范围.
＝
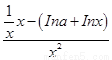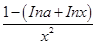，因为 f(x)在[1，＋∞)上为减函数，故 f ′(x)≤0在[1，＋∞)上恒成立，即lna≥1－lnx在[1，＋∞)上恒成立．设φ(x)＝1－lnx，φ(x)max＝1，故lna≥1，a≥e，