题目内容
已知函数 f(x)=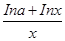 在[1,+∞)上为减函数,求实数a的取值范围.
在[1,+∞)上为减函数,求实数a的取值范围.
【解析】本试题考查了导数在研究函数中的运用。根据函数f(x)=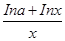 在[1,+∞)上为减函数,可知导函数在给定区间恒小于等于零,f ′(x)≤0在[1,+∞)上恒成立,lna≥1-lnx在[1,+∞)上恒成立.然后利用φ(x)=1-lnx,φ(x)max=1,从而得到a≥e
在[1,+∞)上为减函数,可知导函数在给定区间恒小于等于零,f ′(x)≤0在[1,+∞)上恒成立,lna≥1-lnx在[1,+∞)上恒成立.然后利用φ(x)=1-lnx,φ(x)max=1,从而得到a≥e
f ′(x)=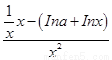 =
=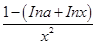 ,因为 f(x)在[1,+∞)上为减函数,故 f ′(x)≤0在[1,+∞)上恒成立,即lna≥1-lnx在[1,+∞)上恒成立.设φ(x)=1-lnx,φ(x)max=1,故lna≥1,a≥e,
,因为 f(x)在[1,+∞)上为减函数,故 f ′(x)≤0在[1,+∞)上恒成立,即lna≥1-lnx在[1,+∞)上恒成立.设φ(x)=1-lnx,φ(x)max=1,故lna≥1,a≥e,
【答案】
a≥e,

练习册系列答案
相关题目
已知函数为f(x)=x2+x-2,其定义域是[-1,2],则这一函数的值域是
[ ]
|
A.[- |
B.[-2,4] |
|
C.[- |
D.(-∞,- |
 ,4]
,4]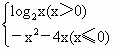 ,则此函数的“友好点对”有
,则此函数的“友好点对”有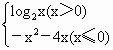 ,则此函数的“友好点对”有
,则此函数的“友好点对”有