题目内容
(本小题满分12分)对某班级50名同学一年来参加社会实践的次数进行的调查统计,得到如下频率分布表:
| 参加次数 | 0 | 1 | 2 | 3 |
| 人数 | 0.1 | 0.2 | 0.4 | 0.3 |
根据上表信息解答以下问题:
(Ⅰ)从该班级任选两名同学,用η表示这两人参加社会实践次数之和,记“函数![]() 在区间
在区间![]() ,
,![]() 内有零点”的事件为
内有零点”的事件为![]() ,求
,求![]() 发生的概率
发生的概率![]() ;
;
(Ⅱ)从该班级任选两名同学,用ξ表示这两人参加社会实践次数之差的绝对值,求随机变量ξ的分布列及数学期望Eξ.
(本小题满分12分)
解:(Ⅰ) 函数![]() 在
在![]() 内单调递增,在区间
内单调递增,在区间![]() 上有零点的条件是
上有零点的条件是![]() 即:
即: 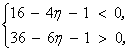
解得:![]() ,所以,
,所以,![]() 或
或![]() ;……………………………………………3分
;……………………………………………3分
![]() ,
,![]() ,……………………5分
,……………………5分
![]() 与
与![]() 为互斥事件,由互斥事件有一个发生的概率公式得:
为互斥事件,由互斥事件有一个发生的概率公式得:
![]() , …………………………………… 6分
, …………………………………… 6分
(Ⅱ) 根据频率分布得到频数分布:
| 参加次数 | 0 | 1 | 2 | 3 |
| 参加人数 | 5 | 10 | 20 | 15 |
从该班级任选两名同学,用![]() 表示这两人参加社会实践次数之差的绝对值,则
表示这两人参加社会实践次数之差的绝对值,则![]() 的可能取
的可能取
值分别是0,1,2,3,………………………………………………………8分
于是:
![]() ,
, ![]() ,
,
![]() ,
, ![]() . …………10分
. …………10分
从而![]() 的分布列如下表:
的分布列如下表:
|
| 0 | 1 | 2 | 3 |
|
|
|
|
|
|
![]() 的数学期望为
的数学期望为![]() . ………………………12分
. ………………………12分

练习册系列答案
相关题目