题目内容
已知函数 是定义在
是定义在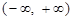 上的偶函数.当
上的偶函数.当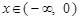 时,
时,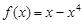 ,则当
,则当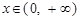 时,
时,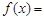 .
.
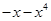
解析试题分析:把 转化为
转化为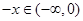 ,利用偶函数的定义
,利用偶函数的定义 即可得所求.
即可得所求.
试题解析: 时,
时,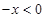 .所以,
.所以,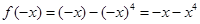 .因为是
.因为是 是定义在
是定义在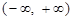 上的偶函数,所以
上的偶函数,所以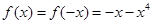 .
.
考点:偶函数,转化与化归思想

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
题目内容
已知函数 是定义在
是定义在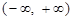 上的偶函数.当
上的偶函数.当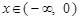 时,
时,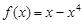 ,则当
,则当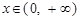 时,
时,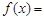 .
.
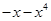
解析试题分析:把 转化为
转化为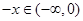 ,利用偶函数的定义
,利用偶函数的定义 即可得所求.
即可得所求.
试题解析: 时,
时,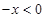 .所以,
.所以,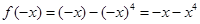 .因为是
.因为是 是定义在
是定义在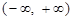 上的偶函数,所以
上的偶函数,所以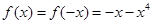 .
.
考点:偶函数,转化与化归思想

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案