题目内容
已知椭圆
与双曲线
（m＞0，n＞0）具有相同的焦点F1，F2，设两曲线的一个交点为Q，∠QF1F2=90°，则双曲线的离心率为 ．
【答案】分析：根据椭圆的方程可求得其半焦距，利用椭圆和双曲线有相同的焦点可求得双曲线的半焦距，把x=3代入椭圆方程求得Q的坐标，利用∠QF1F2=90°推断出QF1⊥x轴，进而可求得|QF1|，利用椭圆的定义求得|QF2|，进而利用双曲线的定义求得双曲线的长轴的长，求得m的值，最后利用e=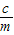
求得答案．
解答：解：根据椭圆方程可得椭圆的半焦距c=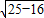
=3
把x=3代入椭圆方程求得y=±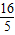
∴|QF1|=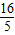
，|QF2|=10-
=
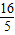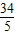
根据双曲线的定义可知2m=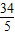
-
=
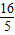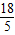
∴m=
∴e=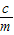
=
故答案为：
点评：本题主要考查了双曲线的简单性质，圆锥曲线的共同特征．考查了学生对圆锥曲线基础知识的综合掌握．
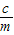求得答案．解答：解：根据椭圆方程可得椭圆的半焦距c=
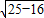=3把x=3代入椭圆方程求得y=±
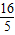
∴|QF1|=
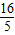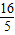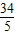
，|QF2|=10-=根据双曲线的定义可知2m=
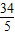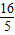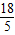
-=∴m=
∴e=
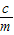=故答案为：
点评：本题主要考查了双曲线的简单性质，圆锥曲线的共同特征．考查了学生对圆锥曲线基础知识的综合掌握．
练习册系列答案
相关题目
与双曲线
（m＞0，n＞0）具有相同的焦点F1，F2，设两曲线的一个交点为Q，∠QF1F2=90°，则双曲线的离心率为 ．
与双曲线
（m＞0，n＞0）有相同的焦点（-c，0）和（c，0），若c是a、m的等比中项，n2是2m2与c2的等差中项，则椭圆的离心率是 ．
与双曲线
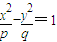（m，n，p，q∈R+）有共同的焦点F1，F2，P是两曲线的一个公共交点．则|PF1|•|PF2|的值是（ ）
与双曲线
（m，n，p，q∈R+）有共同的焦点F1，F2，P是两曲线的一个公共交点．则|PF1|•|PF2|的值是（ ）