题目内容
已知椭圆 与双曲线
与双曲线 (m>0,n>0)有相同的焦点(-c,0)和(c,0),若c是a、m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率是 .
(m>0,n>0)有相同的焦点(-c,0)和(c,0),若c是a、m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率是 .
【答案】分析:由题意得c2=a2-b2=m2+n2=1,c2=am=2,2n2=2m2+c2=3,由此可知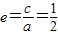 .
.
解答:解:由题意得c2=a2-b2=m2+n2=1 ①,
c2=am=2 ②,
2n2=2m2+c2=3 ③,
将=1 ①代入=3 ③得2n2=3m2+n2,
∴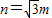 ,代入=3 ③得c=2m,
,代入=3 ③得c=2m,
再代入=2 ②得a=4m,
得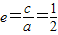 ;
;
故答案为 .
.
点评:本题考查椭圆、双曲线的定义和标准方程,双曲线的离心率.解题时要注意公式的灵活运用.
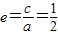 .
.解答:解:由题意得c2=a2-b2=m2+n2=1 ①,
c2=am=2 ②,
2n2=2m2+c2=3 ③,
将=1 ①代入=3 ③得2n2=3m2+n2,
∴
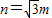 ,代入=3 ③得c=2m,
,代入=3 ③得c=2m,再代入=2 ②得a=4m,
得
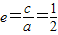 ;
;故答案为
 .
.点评:本题考查椭圆、双曲线的定义和标准方程,双曲线的离心率.解题时要注意公式的灵活运用.

练习册系列答案
相关题目
 与双曲线
与双曲线 (m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 .
(m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 . 与双曲线
与双曲线 (m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 .
(m>0,n>0)具有相同的焦点F1,F2,设两曲线的一个交点为Q,∠QF1F2=90°,则双曲线的离心率为 . 与双曲线
与双曲线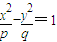 (m,n,p,q∈R+)有共同的焦点F1,F2,P是两曲线的一个公共交点.则|PF1|•|PF2|的值是( )
(m,n,p,q∈R+)有共同的焦点F1,F2,P是两曲线的一个公共交点.则|PF1|•|PF2|的值是( ) 与双曲线
与双曲线 (m,n,p,q∈R+)有共同的焦点F1,F2,P是两曲线的一个公共交点.则|PF1|•|PF2|的值是( )
(m,n,p,q∈R+)有共同的焦点F1,F2,P是两曲线的一个公共交点.则|PF1|•|PF2|的值是( )