题目内容
(本小题满分12分)
已知M(-3,0)﹑N(3,0),P为坐标平面上的动点,且直线PM与直线PN的斜率之积为常数m(m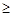 -1,m
-1,m 0).
0).
(1)求P点的轨迹方程并讨论轨迹是什么曲线?
(2)若 , P点的轨迹为曲线C,过点Q(2,0)斜率为
, P点的轨迹为曲线C,过点Q(2,0)斜率为 的直线
的直线 与曲线C交于不同的两点A﹑B,AB中点为R,直线OR(O为坐标原点)的斜率为
与曲线C交于不同的两点A﹑B,AB中点为R,直线OR(O为坐标原点)的斜率为 ,求证
,求证 为定值;
为定值;
(3)在(2)的条件下,设 ,且
,且 ,求
,求 在y轴上的截距的变化范围.
在y轴上的截距的变化范围.

【答案】
解:(1)由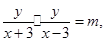 得
得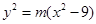 ,
,
若m= -1,则方程为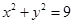 ,轨迹为圆(除A B点)
,轨迹为圆(除A B点)
若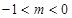 ,方程为
,方程为 ,轨迹为椭圆(除A B点);
,轨迹为椭圆(除A B点);
若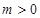 ,方程为
,方程为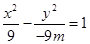 ,轨迹为双曲线(除A B点)。
,轨迹为双曲线(除A B点)。
(2)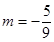 时,曲线C方程为
时,曲线C方程为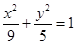 ,设
,设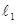 的方程为:
的方程为: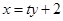
与曲线C方程联立得: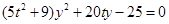 ,…………6分
,…………6分
设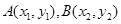 ,则
,则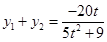 ①,
①,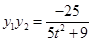 ②,
②,
可得 ,
,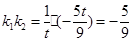 。
。
(3)由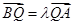 得
得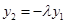 代入①②得:
代入①②得:
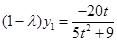 ③,
③,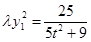 ④,
④,
③式平方除以④式得: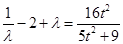 ,
,
而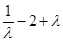 在
在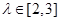 上单调递增,
上单调递增,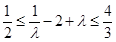 ,
,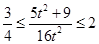 ,
,
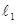 在y轴上的截距为b,
在y轴上的截距为b,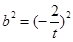 =
=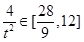 ,
,
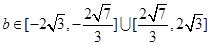 。
。
【解析】略

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目