题目内容
已知:z∈C,且|z|=1,设u=(3+4i)z+(3-4i)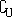 ,
,
(Ⅰ)证明u是实数;
(Ⅱ)求u的最大值和最小值.
答案:
解析:
解析:
|
已知z∈C,且|z|=1,设u=(3+4i)z+(3-4i) (Ⅰ)证法(一) ∵ ∴u∈R. 证法(二): 设z=x+yi,则 ∴u=(3+4i)(x+yi)+(3-4i)(x-yi) =3x-4y+(4x+3y)i+3x-4y-(4x+3y)i=6x-8y ∴u∈R. (Ⅱ)解:由|z|=1,可设z=cosθ+isinθ 则u=3(z+
=10cos ∴u的最大值为10,u的最小值为-10. |

练习册系列答案
相关题目
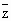 )+4i(z-
)+4i(z-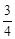 B.
B.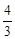 C.-
C.-