题目内容
已知函数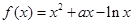 ,
,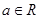 ;
;
(Ⅰ)若函数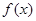 在[1,2]上是减函数,求实数
在[1,2]上是减函数,求实数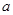 的取值范围;
的取值范围;
(Ⅱ)令 ,是否存在实数
,是否存在实数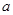 ,当
,当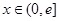 (
(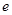 是自然对数的底数)时,函数
是自然对数的底数)时,函数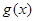 的最小值是
的最小值是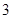 .若存在,求出
.若存在,求出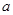 的值;若不存在,说明理由.
的值;若不存在,说明理由.
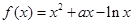 ,
,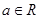 ;
;(Ⅰ)若函数
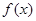 在[1,2]上是减函数,求实数
在[1,2]上是减函数,求实数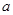 的取值范围;
的取值范围;(Ⅱ)令
 ,是否存在实数
,是否存在实数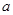 ,当
,当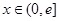 (
(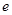 是自然对数的底数)时,函数
是自然对数的底数)时,函数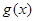 的最小值是
的最小值是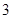 .若存在,求出
.若存在,求出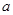 的值;若不存在,说明理由.
的值;若不存在,说明理由.(Ⅰ)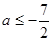 ;(Ⅱ)
;(Ⅱ)
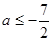 ;(Ⅱ)
;(Ⅱ)
试题分析:(Ⅰ)根据原函数的单调性转化为导数来求;(Ⅱ)利用导数分析单调性,进而求最值.
试题解析:(Ⅰ)若函数
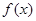 在[1,2]上是减函数,
在[1,2]上是减函数,则
 在[1,2]上恒成立
在[1,2]上恒成立令h(x)=2x2+ax-1,x∈[1,2],∴h(x)≤0在[1,2]上恒成立
∴
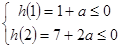 得
得 ,∴a≤
,∴a≤ 6分
6分(Ⅱ)假设存在实数a,使g(x)=f(x)-x2,x∈(0,e]有最小值3
g(x)=ax-lnx,x∈(0,e],g′(x)=a-
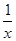 =
=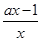
①当a≤0时,g′(x)<0,g(x)在(0,e]上单调递减
∴g(x)min=g(e)=ae-1=3,∴a=
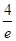 (舍去)
(舍去) ②当0<
 <e即a>
<e即a> 时,在(0,
时,在(0, )上,g′(x)<0;在(
)上,g′(x)<0;在( ,e]上,g′(x)>0
,e]上,g′(x)>0∴g(x)在(0,
 ]上单调递减,在(
]上单调递减,在( ,e]上单调递增
,e]上单调递增∴g(x)min=g
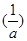 =1+lna=3,∴a=e2满足条件
=1+lna=3,∴a=e2满足条件③当
 ≥e即0<a≤
≥e即0<a≤ 时,g′(x)<0,g(x)在(0,e]上单调递减
时,g′(x)<0,g(x)在(0,e]上单调递减g(x)min=g(e)=ae-1=3
∴a=
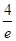 >
> (舍去)
(舍去)综上所述,存在a=e2使得当x∈(0,e]时,g(x)有最小值3 .15分

练习册系列答案
相关题目
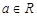 ,函数
,函数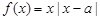 .
.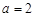 时,写出函数
时,写出函数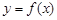 的单调递增区间;
的单调递增区间;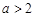 时,求函数
时,求函数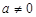 ,函数
,函数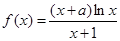 ,曲线
,曲线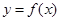 在点
在点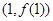 处的切线与直线
处的切线与直线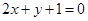 垂直.
垂直.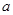 的值;
的值;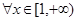 ,
,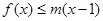 恒成立,求
恒成立,求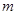 的范围.
的范围.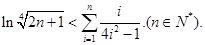
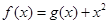 ,曲线
,曲线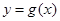 在点
在点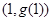 处的切线方程为
处的切线方程为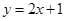 ,则曲线
,则曲线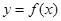 在点
在点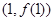 处切线的斜率为( )
处切线的斜率为( )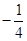
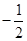
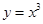 和
和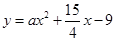 都相切,则
都相切,则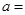 ( )
( )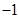 或
或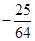
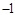 或
或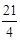
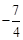 或
或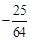
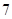
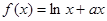 存在与直线
存在与直线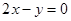 平行的切线,则实数
平行的切线,则实数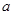 的取值范围是( )
的取值范围是( )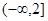
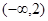
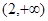
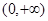
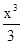 +
+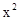 -3x—4在[0,2]上的最小值是
-3x—4在[0,2]上的最小值是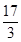
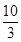
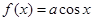 与曲线
与曲线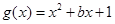 在交点
在交点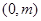 处有公切线, 则
处有公切线, 则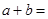 ( )
( )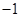

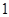
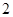
 的单调递减区间是
的单调递减区间是