题目内容
已知数列{an}中,a1=2,n∈N*,an>0,数列{an}的前n项和为Sn,且满足an+1=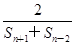 .
.
(1)求{Sn}的通项公式;
(2)设{bk}是{Sn}中的按从小到大顺序组成的整数数列.
①求b3;
②存在N(N∈N*),当n≤N时,使得在{Sn}中,数列{bk}有且只有20项,求N的范围.
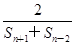 .
.(1)求{Sn}的通项公式;
(2)设{bk}是{Sn}中的按从小到大顺序组成的整数数列.
①求b3;
②存在N(N∈N*),当n≤N时,使得在{Sn}中,数列{bk}有且只有20项,求N的范围.
(1)Sn=1+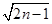 (2)①6②N∈[761,840]
(2)①6②N∈[761,840]
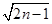 (2)①6②N∈[761,840]
(2)①6②N∈[761,840](1)an+1=Sn+1-Sn,
∴(Sn+1-Sn)(Sn+1+Sn-2)=2;即(Sn+1)2-(Sn)2-2(Sn+1-Sn)=2,
∴(Sn+1-1)2-(Sn-1)2=2,且(S1-1)2=1,∴{(Sn-1)2}是首项为1,公差为2的等差数列,
∴Sn=1+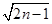 .
.
(2)①n=1时,S1=1+1=2=b1,n=5时,S5=1+3=4=b2,n=13时,S13=1+5=6=b3.
②∵2n-1是奇数,Sn=1+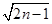 为有理数,则
为有理数,则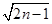 =2k-1,
=2k-1,
∴n=2k2-2k+1,当k=20时,n=761;当k=21时,n=841;
∴存在N∈[761,840],当n≤N时,使得在{Sn}中,数列{bk}有且只有20项.
∴(Sn+1-Sn)(Sn+1+Sn-2)=2;即(Sn+1)2-(Sn)2-2(Sn+1-Sn)=2,
∴(Sn+1-1)2-(Sn-1)2=2,且(S1-1)2=1,∴{(Sn-1)2}是首项为1,公差为2的等差数列,
∴Sn=1+
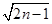 .
.(2)①n=1时,S1=1+1=2=b1,n=5时,S5=1+3=4=b2,n=13时,S13=1+5=6=b3.
②∵2n-1是奇数,Sn=1+
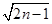 为有理数,则
为有理数,则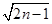 =2k-1,
=2k-1,∴n=2k2-2k+1,当k=20时,n=761;当k=21时,n=841;
∴存在N∈[761,840],当n≤N时,使得在{Sn}中,数列{bk}有且只有20项.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 为数列
为数列 的前
的前 项和,对任意的
项和,对任意的 ,都有
,都有
 为常数,且
为常数,且 .
. ,数列
,数列 满足
满足
 ,
, ,求数列
,求数列 的通项公式;
的通项公式; 的前
的前 .
.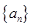 和
和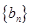 的前
的前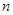 项和分别为
项和分别为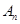 和
和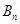 ,且
,且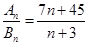 ,则使得
,则使得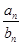 为正偶数时,
为正偶数时,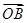 =a100·
=a100·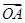 +a101
+a101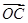 ,且A、B、C三点共线(该直线不过点O),则S200=________.
,且A、B、C三点共线(该直线不过点O),则S200=________.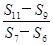 =________.
=________. <-1,且它们的前n项和Sn有最大值,求使得Sn<0的n的最小值.
<-1,且它们的前n项和Sn有最大值,求使得Sn<0的n的最小值. 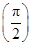 =0.
=0.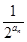 ),求数列{bn}的前n项和Sn.
),求数列{bn}的前n项和Sn. 是等比数列,数列
是等比数列,数列 是等差数列,则
是等差数列,则 的值为 .
的值为 .