题目内容
 圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知点P(x0,y0)、M(m,n)是圆锥曲线C上不与顶点重合的任意两点,MN是垂直于x轴的一条垂轴弦,直线MP、NP分别交x轴于点E(xE,0)和点F(xF,0).
圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知点P(x0,y0)、M(m,n)是圆锥曲线C上不与顶点重合的任意两点,MN是垂直于x轴的一条垂轴弦,直线MP、NP分别交x轴于点E(xE,0)和点F(xF,0).(1)试用x0,y0,m,n的代数式分别表示xE和xF;
(2)若C的方程为
| x2 |
| a2 |
| y2 |
| b2 |
(3)请选定一条除椭圆外的圆锥曲线C,试探究xE和xF经过某种四则运算(加、减、乘、除),其结果是否是与MN和点P位置无关的定值,写出你的研究结论并证明.
分析:(1)求出PM 直线的方程,令y=0,求出xE,同理求得xF .
(2)由(1)可知:xE•xF=
.把M,P坐标代入椭圆的方程,求出n2,y02 代入
xE•xF的式子,化简可得结论.
(3)第一层次:①点P是圆C:x2+y2=R2上不与坐标轴重合的任意一点,MN是垂直于x轴的垂轴弦,
直线MP、NP分别交x轴于点E(xE,0)和点F(xF,0),则xE•xF =R2 .证法同(2).
②点P是双曲线C:
-
=1(a>0,b>0)上不与顶点重合的任意一点,MN是垂直于x轴的垂轴弦,
直线MP、NP分别交x轴于点E(xE,0)和点F(xF,0),则xE•xF=a2 .证法同(2).
第二层次:点P是抛物线C:y2=2px(p>0)上不与顶点重合的任意一点,MN是垂直于x轴的垂轴弦,
直线MP、NP分别交x轴于点E(xE,0)和点F(xF,0),则xE+xF =0.
(2)由(1)可知:xE•xF=
| m2y02-n2x02 |
| y02-n2 |
xE•xF的式子,化简可得结论.
(3)第一层次:①点P是圆C:x2+y2=R2上不与坐标轴重合的任意一点,MN是垂直于x轴的垂轴弦,
直线MP、NP分别交x轴于点E(xE,0)和点F(xF,0),则xE•xF =R2 .证法同(2).
②点P是双曲线C:
| x2 |
| a2 |
| y2 |
| b2 |
直线MP、NP分别交x轴于点E(xE,0)和点F(xF,0),则xE•xF=a2 .证法同(2).
第二层次:点P是抛物线C:y2=2px(p>0)上不与顶点重合的任意一点,MN是垂直于x轴的垂轴弦,
直线MP、NP分别交x轴于点E(xE,0)和点F(xF,0),则xE+xF =0.
解答:解:(1)因为MN是垂直于x轴的一条垂轴弦,所以,N(m,-n),
则lMP:y-n=
(x-m). 令y=0,则xE=
.
同理可得:xF=
.
(2)由(1)可知:xE•xF=
.∵M,P在椭圆C:
+
=1上,
∴n2=b2(1-
),y02=b2(1-
),
则xE•xF=
=
=a2(定值)
∴xE•xF是与MN和点P位置无关的定值.
(3)第一层次:
①点P是圆C:x2+y2=R2上不与坐标轴重合的任意一点,MN是垂直于x轴的垂轴弦,直线MP、NP分别交x轴于点E(xE,0)和点F(xF,0),则xE•xF =R2 .
证明如下:由(1)知:xE•xF=
,∵M,P在圆C:x2+y2=R2上,
∴n2=R2-m2,y02=R2-x02,则xE•xF=
=
=R2,
∴xE•xF是与MN和点P位置无关的定值.
②点P是双曲线C:
-
=1(a>0,b>0)上不与顶点重合的任意一点,MN是垂直于x轴的垂轴弦,
直线MP、NP分别交x轴于点E(xE,0)和点F(xF,0),则xE•xF=a2 .
证明如下:由(1)知:xE•xF=
,∵M,P在双曲线C:
-
=1上,
∴n2=b2(
-1),y02=b2(
-1),
则xE•xF=
=
=a2
∴xE•xF是与MN和点P位置无关的定值.
第二层次:
点P是抛物线C:y2=2px(p>0)上不与顶点重合的任意一点,MN是垂直于x轴的垂轴弦,
直线MP、NP分别交x轴于点E(xE,0)和点F(xF,0),则xE+xF =0.
证明如下:由(1)知:xE+xF=
,∵M,P在抛物线C:y2=2px(p>0)上,
∴y02=2px0,n2=2pm,则xE+xF=
=
=0,
∴xE+xF是与MN和点P位置无关的定值.
则lMP:y-n=
| y0-n |
| x0-m |
| my0-nx0 |
| y0-n |
同理可得:xF=
| my0+nx0 |
| y0+n |
(2)由(1)可知:xE•xF=
| m2y02-n2x02 |
| y02-n2 |
| x2 |
| a2 |
| y2 |
| b2 |
∴n2=b2(1-
| m2 |
| a2 |
| x02 |
| a2 |
则xE•xF=
m2b2(1-
| ||||
b2(1-
|
| b2(m2-x02) | ||
|
∴xE•xF是与MN和点P位置无关的定值.
(3)第一层次:
①点P是圆C:x2+y2=R2上不与坐标轴重合的任意一点,MN是垂直于x轴的垂轴弦,直线MP、NP分别交x轴于点E(xE,0)和点F(xF,0),则xE•xF =R2 .
证明如下:由(1)知:xE•xF=
| m2y02-n2x02 |
| y02-n2 |
∴n2=R2-m2,y02=R2-x02,则xE•xF=
| m2(R2-x02)-(R2-m2)x02 |
| (R2-x02)-(R2-m2) |
| R2(m2-x02) |
| (m2-x02) |
∴xE•xF是与MN和点P位置无关的定值.
②点P是双曲线C:
| x2 |
| a2 |
| y2 |
| b2 |
直线MP、NP分别交x轴于点E(xE,0)和点F(xF,0),则xE•xF=a2 .
证明如下:由(1)知:xE•xF=
| m2y02-n2x02 |
| y02-n2 |
| x2 |
| a2 |
| y2 |
| b2 |
∴n2=b2(
| m2 |
| a2 |
| x02 |
| a2 |
则xE•xF=
m2b2(
| ||||
b2(
|
| b2(x02-m2) | ||
|
∴xE•xF是与MN和点P位置无关的定值.
第二层次:
点P是抛物线C:y2=2px(p>0)上不与顶点重合的任意一点,MN是垂直于x轴的垂轴弦,
直线MP、NP分别交x轴于点E(xE,0)和点F(xF,0),则xE+xF =0.
证明如下:由(1)知:xE+xF=
| 2(my02-n2x0) |
| y02-n2 |
∴y02=2px0,n2=2pm,则xE+xF=
| 2(my02-n2x0) |
| y02-n2 |
| 2(m2px0-2pmx0) |
| y02-n2 |
∴xE+xF是与MN和点P位置无关的定值.
点评:本题考查椭圆、圆、双曲线、抛物线的简单性质,以及求直线和二次曲线的交点坐标的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知椭圆C:
圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知椭圆C: 圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知点P(
圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知点P(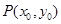 、
、 是圆锥曲线C
是圆锥曲线C 上不与顶点重合的任意两点,
上不与顶点重合的任意两点, 是垂直于
是垂直于 轴的一条垂轴弦,直线
轴的一条垂轴弦,直线 分别交
分别交 和点
和点 。
。
 的代数式分别表示
的代数式分别表示 和
和 ;
; (如图),求证:
(如图),求证: 是与
是与 位置无关的定值;
位置无关的定值; 结果是否是与
结果是否是与 ”.类比这一结论,我们猜想:“若曲线C的方程为
”.类比这一结论,我们猜想:“若曲线C的方程为 (如图),则xE•xF也是与点M、N、P位置无关的定值”,请你对该猜想给出证明.
(如图),则xE•xF也是与点M、N、P位置无关的定值”,请你对该猜想给出证明.