题目内容
y=f（x）的图象是由F的图象按向量
=（-1，2）平移后得到的，若F的函数解析式为y=
（x≠0），则y=f（x）的反函数的解析式为
- A.y=
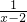-1（x∈R且x≠2） - B.y=
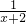+1（x∈R且x≠-2） - C.y=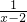+1（x∈R且x≠2）
- D.y=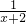+1（x∈R且x≠-2）
A
分析：先根据向量的方向，然后按照左加右减的原则进行平移可得f（x）的函数式，再从函数式y=f（x）的中反解出x，将x，y互换即得，注意反函数的定义域即为原函数的值域，即可得到原函数的反函数（注意指明定义域）．
解答：将函数y=（x≠0）的图象按向量=（-1，2）平移后得到
y=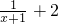
，即f（x）=，
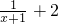由函数y=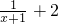解得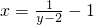 
（y≠2），
∴原函数的反函数是y=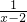-1（x∈R且x≠2）
故选A．
点评：本题主要考查函数的图象与图象变化、函数按向量方向的平移、反函数等知识点，图象变化是高考的常考点，需要同学们熟练掌握．
分析：先根据向量
的方向，然后按照左加右减的原则进行平移可得f（x）的函数式，再从函数式y=f（x）的中反解出x，将x，y互换即得，注意反函数的定义域即为原函数的值域，即可得到原函数的反函数（注意指明定义域）．解答：将函数y=
（x≠0）的图象按向量=（-1，2）平移后得到y=
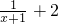，即f（x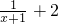）=，由函数y=
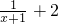解得 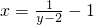（y≠2），∴原函数的反函数是y=
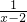-1（x∈R且x≠2）故选A．
点评：本题主要考查函数的图象与图象变化、函数按向量方向的平移、反函数等知识点，图象变化是高考的常考点，需要同学们熟练掌握．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
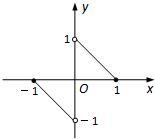函数y=f（x）的图象是两条直线的一部分（如图所示），其定义域为[-1，0）∪（0，1]，则不等式f（x）-f（-x）＞-1的解集为
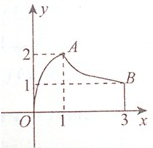如图，函数y=f（x）的图象是曲线OAB，其中点O（0，0），A（1，2），B（3，1），则