题目内容
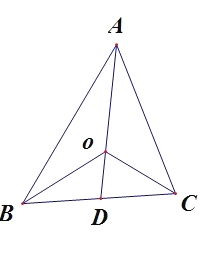
【题目】在![]() 中,给出如下命题:
中,给出如下命题:
①![]() 是
是![]() 所在平面内一定点,且满足
所在平面内一定点,且满足![]() ,则
,则![]() 是
是![]() 的垂心;
的垂心;
②![]() 是
是![]() 所在平面内一定点,动点
所在平面内一定点,动点![]() 满足
满足![]() ,
,![]() ,则动点
,则动点![]() 一定过
一定过![]() 的重心;
的重心;
③![]() 是
是![]() 内一定点,且
内一定点,且![]() ,则
,则![]() ;
;
④若 且
且 ,则
,则![]() 为等边三角形,
为等边三角形,
其中正确的命题为_____(将所有正确命题的序号都填上)
【答案】①②④.
【解析】
①:运用已知的式子进行合理的变形,可以得到![]() ,进而得到
,进而得到![]() ,再次运用等式同样可以得到
,再次运用等式同样可以得到![]() ,
,![]() ,这样可以证明出
,这样可以证明出![]() 是
是![]() 的垂心;
的垂心;
②:运用平面向量的减法的运算法则、加法的几何意义,结合平面向量共线定理,可以证明本命题是真命题;
③:运用平面向量的加法的几何意义以及平面向量共线定理,结合面积公式,可证明出本结论是错误的;
④:运用平面向量的加法几何意义和平面向量的数量积的定义,可以证明出本结论是正确的.
①: ![]() ,同理可得:
,同理可得:![]() ,
,![]() ,所以本命题是真命题;
,所以本命题是真命题;
②: ![]() ,设
,设![]() 的中点为
的中点为![]() ,所以有
,所以有![]() ,因此动点
,因此动点![]() 一定过
一定过![]() 的重心,故本命题是真命题;
的重心,故本命题是真命题;
③: 由![]() ,可得设
,可得设![]() 的中点为
的中点为![]() ,
,![]() ,
,
![]() ,故本命题是假命题;
,故本命题是假命题;
④: 由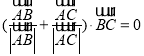 可知角
可知角![]() 的平分线垂直于底边,故
的平分线垂直于底边,故![]() 是等腰三角形,
是等腰三角形,
由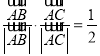 可知:
可知:![]() ,所以
,所以![]() 是等边三角形,故本命题是真命题,因此正确的命题为①②④.
是等边三角形,故本命题是真命题,因此正确的命题为①②④.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:

(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数![]() ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的工人数填入下面的列联表:
的工人数填入下面的列联表:
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:![]() ,
,
|
|
|
|
|
|
|
|
