题目内容
 已知定义在R上的函数f(x)=asinωx+bcosωx(ω>0,a>0,b>0)周期为
已知定义在R上的函数f(x)=asinωx+bcosωx(ω>0,a>0,b>0)周期为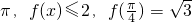 .
.
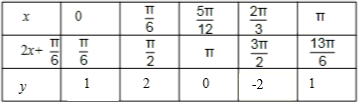
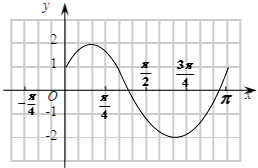
(1)写出f(x)的表达式,并作出f(x)在[0,π]上的简图;
(2)写出函数f(x)的单调递增区间;
(3)说明f(x)的图象如何由函数y=sinx的图象经过变换得到.
解:(1)∵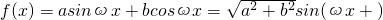 ,
,
∴T=π,f(x)≤2,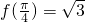 .
.
∴ ,
,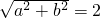 ,
,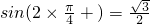 即
即 ,
,
∴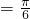 ,
,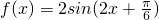
(2)由正弦的单调增区间可知: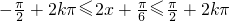 ,解得
,解得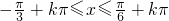 ,即在每个闭区间
,即在每个闭区间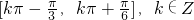 单调递增
单调递增
(3)将函数y=2sinx的图象向左平移 个单位,再将得到的函数图象上的所有的点的纵坐标不变,横坐标缩短为原来的
个单位,再将得到的函数图象上的所有的点的纵坐标不变,横坐标缩短为原来的
分析:(1)函数f(x)的表达式化为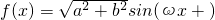 ,通过周期,最值以及
,通过周期,最值以及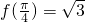 ,求出函数的表达式,直接作出f(x)在[0,π]上的简图;
,求出函数的表达式,直接作出f(x)在[0,π]上的简图;
(2)利用正弦函数的单调增区间直接求出函数f(x)的单调递增区间;
(3)函数y=sinx的图象经过向左平移,再将得到的函数图象上的所有的点的纵坐标不变,横坐标缩短为原来的 ,纵坐标变为原来的2倍,得到结果.
,纵坐标变为原来的2倍,得到结果.
点评:本题考查三角函数的解析式的求法,求三角函数的单调性,注意函数图象的平移,五点法作图的基本方法.考查计算能力.
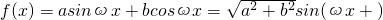 ,
,∴T=π,f(x)≤2,
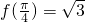 .
.∴
 ,
,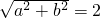 ,
,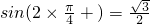 即
即 ,
,∴
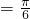 ,
,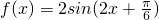


(2)由正弦的单调增区间可知:
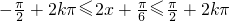 ,解得
,解得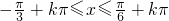 ,即在每个闭区间
,即在每个闭区间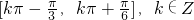 单调递增
单调递增(3)将函数y=2sinx的图象向左平移
 个单位,再将得到的函数图象上的所有的点的纵坐标不变,横坐标缩短为原来的
个单位,再将得到的函数图象上的所有的点的纵坐标不变,横坐标缩短为原来的
分析:(1)函数f(x)的表达式化为
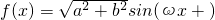 ,通过周期,最值以及
,通过周期,最值以及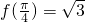 ,求出函数的表达式,直接作出f(x)在[0,π]上的简图;
,求出函数的表达式,直接作出f(x)在[0,π]上的简图;(2)利用正弦函数的单调增区间直接求出函数f(x)的单调递增区间;
(3)函数y=sinx的图象经过向左平移,再将得到的函数图象上的所有的点的纵坐标不变,横坐标缩短为原来的
 ,纵坐标变为原来的2倍,得到结果.
,纵坐标变为原来的2倍,得到结果.点评:本题考查三角函数的解析式的求法,求三角函数的单调性,注意函数图象的平移,五点法作图的基本方法.考查计算能力.

练习册系列答案
相关题目
已知定义在R上的函数f(x),对任意x∈R,都有f(x+6)=f(x)+f(3)成立,若函数y=f(x+1)的图象关于直线x=-1对称,则f(2013)=( )
| A、0 | B、2013 | C、3 | D、-2013 |