题目内容
设f
(x)=∣x-1∣,f
,函数g(x)是这样定义的:当f
时，g(x)= f(x),当f(x)<f
时，g(x)= f,若方程g(x)=a有四个不同的实数解,则实数a的取值范围是( )
(x)=∣x-1∣,f,函数g(x)是这样定义的:当f时，g(x)= f(x),当f(x)<f时，g(x)= f,若方程g(x)=a有四个不同的实数解,则实数a的取值范围是( )| A．a<4 | B．0<a<4 | C．0<a<3 | D．3<a<4 |
D
解：f1（x）=|x-1|，f2（x）=-x2+6x-5的图象如图，
函数g（x）的图象为两函数中位置在上的部分，即
g(x)= -x+1 (x≤1)
-x2+6x-5 (1＜x≤4)
x-1 (x＞4)
由 y="x" y=-x2+6x-5 得A（4，3），f2（x）=-x2+6x-5的顶点坐标为B（3，4）
要使方程g（x）=a有四个不同的实数解，即函数g（x）的图象与函数y=a的图象有四个不同交点
数形结合可得3＜a＜4
故选D
函数g（x）的图象为两函数中位置在上的部分，即
g(x)= -x+1 (x≤1)
-x2+6x-5 (1＜x≤4)
x-1 (x＞4)
由 y="x" y=-x2+6x-5 得A（4，3），f2（x）=-x2+6x-5的顶点坐标为B（3，4）
要使方程g（x）=a有四个不同的实数解，即函数g（x）的图象与函数y=a的图象有四个不同交点
数形结合可得3＜a＜4
故选D
练习册系列答案
相关题目
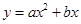与指数函数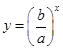
的图象只可能是（ ）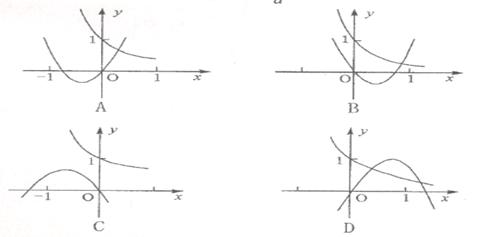
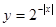的图象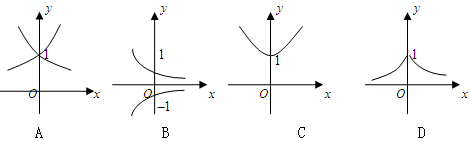是（ ）
的图象可能是（ ）
与乘客量
之间关系的图象．由于目前该条公交线路亏损，公司有关人员提出了
为常数，抛物线
，则当
时，在平面直角坐标系中图像最恰当的是（这里省略了坐标轴）（ ）
的图象恒过定点
，则点
(
为参数)所表示的曲线是 ( )
的大致图象是（ ）