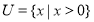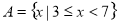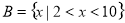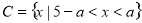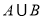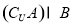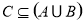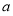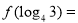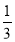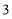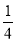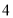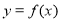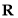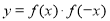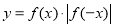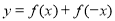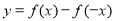题目内容
定义在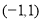 上的函数
上的函数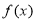 满足:①对任意
满足:①对任意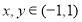 都有:
都有: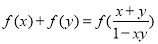 ;②当
;②当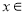
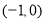 时,
时,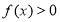 ,回答下列问题.
,回答下列问题.
(1)证明:函数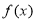 在
在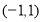 上的图像关于原点对称;
上的图像关于原点对称;
(2)判断函数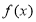 在
在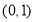 上的单调性,并说明理由.
上的单调性,并说明理由.
(3)证明: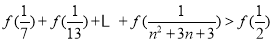 ,
,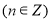 .
.
【解析】
试题分析:(1)利用条件①,令 得出
得出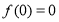 ,令
,令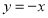 ,得出
,得出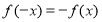 ,因此
,因此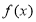 是
是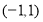 上的奇函数,其图像关于原点对称;(2)利用单调性定义进行判断,结合第(1)小题的结论进行化简和①②两个条件对结果的符号进行判断;(3)结合条件①把左边式子的第
上的奇函数,其图像关于原点对称;(2)利用单调性定义进行判断,结合第(1)小题的结论进行化简和①②两个条件对结果的符号进行判断;(3)结合条件①把左边式子的第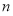 项化为
项化为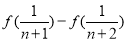 ,由此左边可以化为
,由此左边可以化为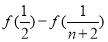 ,再利用第(2)小题的结论得出
,再利用第(2)小题的结论得出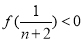 ,原不等式得证.
,原不等式得证.
试题解析:(1)令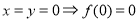 ,
,
令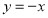 ,则
,则 .
.
所以,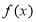 在
在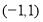 上是奇函数. 4分
上是奇函数. 4分
(2)设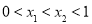 ,则
,则
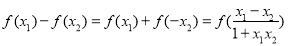 , 6分
, 6分
而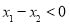 ,
,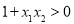
 , 7分
, 7分
即当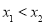 时,
时,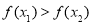 .
.
∴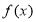 在
在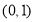 上单调递减. 8分
上单调递减. 8分
(3)
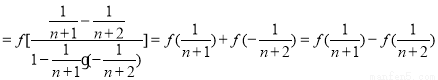
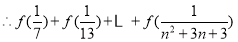
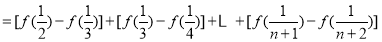
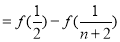 ,
,
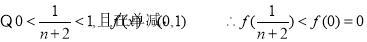 ,
,
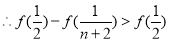 .
.
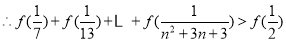 . 13分
. 13分
考点:函数的奇偶性、单调性,转化与化归思想.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目