题目内容
(2012•朝阳区二模)若实数x,y满足
则x2+y2的最小值是
.
|
| 1 |
| 2 |
| 1 |
| 2 |
分析:根据已知条件实数x,y满足
则,画出可行域,将x2+y2的最小值转化为可行域中的点到原点的最小距离的平方,从而求解;
|
解答: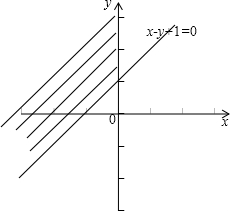 解:由已知条件实数x,y满足
解:由已知条件实数x,y满足
画出可行域,如下图:
求x2+y2的最小值,目标函数z=x2+y2,即是图中可行域中的点到原点的最小距离的平方,
可知原点0到直线x-y+1=0的最短距离d=
=
,
∴x2+y2的最小值为d2=
,
故答案为
;
 解:由已知条件实数x,y满足
解:由已知条件实数x,y满足
|
求x2+y2的最小值,目标函数z=x2+y2,即是图中可行域中的点到原点的最小距离的平方,
可知原点0到直线x-y+1=0的最短距离d=
| |1| | ||
|
| ||
| 2 |
∴x2+y2的最小值为d2=
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
点评:本题只是直接考查线性规划问题,是一道跟以前若有区别的题,要学会寻找目标函数并进行转化,近年来高考线性规划问题高考数学考试的热点,数形结合是数学思想的重要手段之一,是连接代数和几何的重要方法.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目