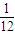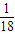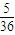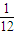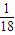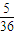题目内容
已知函数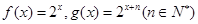 ,点
,点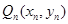 、
、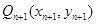 在函数
在函数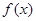 的图象上,
的图象上,
点 在函数
在函数 的图象上,设
的图象上,设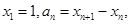
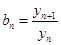 .
.
(1)求数列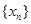 的通项公式;
的通项公式;
(2)记 ,求数列
,求数列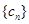 的前
的前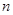 项和为
项和为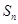 ;
;
(3)已知 ,记数列
,记数列 的前
的前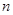 项和为
项和为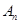 ,数列
,数列 的前
的前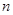 项和为
项和为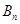 ,试比较
,试比较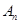 与
与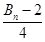 的大小.
的大小.
【答案】
(1)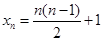 ;
;
(2)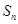
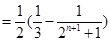 ;
;
(3)当 时,
时,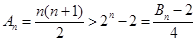 ;
;
当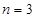 时,
时,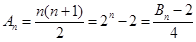 ;
;
当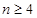 时,
时,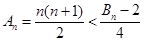 .
.
【解析】
试题分析:(1)把点点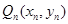 、
、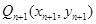 代入
代入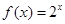 中,点
中,点 代入函数
代入函数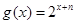 中,可得
中,可得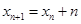 ,然后利用叠加的方法求的
,然后利用叠加的方法求的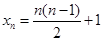 ;(2)由
;(2)由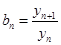 和
和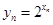 可得
可得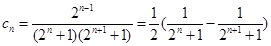 ,然后利用裂项法求数列
,然后利用裂项法求数列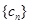 的前
的前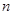 项和
项和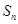 即可;(3)由
即可;(3)由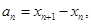 得
得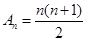 ,由
,由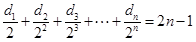 可得
可得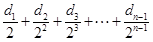
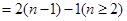
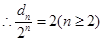 ,即
,即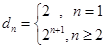 ,求出
,求出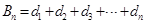
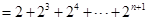
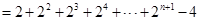 ,即
,即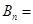
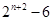 ,所以
,所以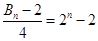 最后分类讨论比较
最后分类讨论比较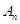 与
与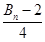 的大小即可.
的大小即可.
试题解析:(1)由题有: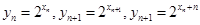
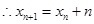
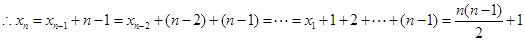 3分
3分
(2)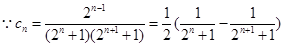 ,
,
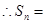
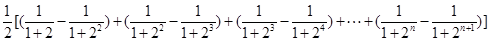
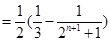 8分
8分
(3)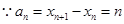 ,
,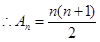 ,
,
由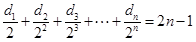 知
知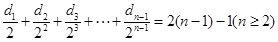
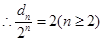 ,
而
,
而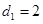 ,所以可得
,所以可得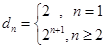 .
.
于是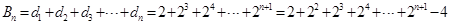
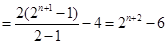 .
.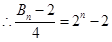
当 时
时
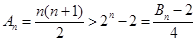 ;
;
当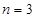 时,
时,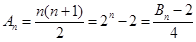
当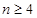 时,
时,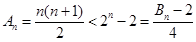
下面证明:当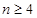 时,
时,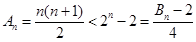
证法一:(利用组合恒等式放缩)
当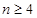 时,
时,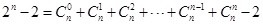
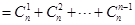
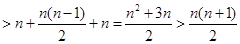
∴当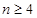 时,
时,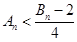 13分
13分
证法二:(数学归纳法)证明略
证法三:(函数法)∵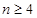 时,
时,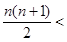
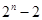
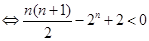
构造函数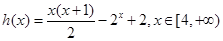 ,
,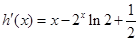
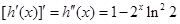 ∴当
∴当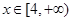 时,
时,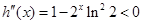
∴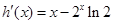 在区间
在区间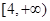 是减函数,
是减函数,
∴当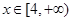 时,
时,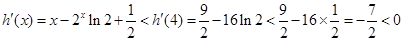
∴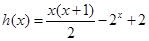 在区间
在区间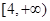 是减函数,
是减函数,
∴当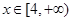 时,
时,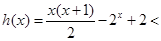
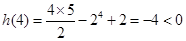
从而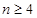 时,
时,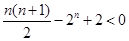 ,即
,即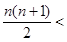
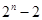 ∴当
∴当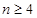 时,
时,
考点:1.点与曲线的位置关系;2.数列的通项公式和前n项和;3.不等式的证明.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目