题目内容
【题目】如图1, ![]() ,
, ![]() ,过动点A作
,过动点A作![]() ,垂足D在线段BC上且异于点B,连接AB,沿
,垂足D在线段BC上且异于点B,连接AB,沿![]() 将△
将△![]() 折起,使
折起,使![]() (如图2所示).
(如图2所示).

(1)当![]() 的长为多少时,三棱锥
的长为多少时,三棱锥![]() 的体积最大;
的体积最大;
(2)当三棱锥![]() 的体积最大时,设点
的体积最大时,设点![]() ,
, ![]() 分别为棱
分别为棱![]() ,
, ![]() 的中点,试在棱
的中点,试在棱![]() 上确定一点
上确定一点![]() ,使得
,使得![]()
![]() ,并求
,并求![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
【答案】(1)![]() 时,三棱锥
时,三棱锥![]() 的体积最大.(2)当
的体积最大.(2)当![]() 时,
时, ![]() .
. ![]() 与平面
与平面![]() 所成角的大小
所成角的大小![]() .
.
【解析】试题分析:(1)设![]() ,则
,则![]() .又
.又![]() ,所以
,所以![]() .由此易将三棱锥
.由此易将三棱锥![]() 的体积表示为
的体积表示为![]() 的函数,通过求函数的最值的方法可求得它的最大值.
的函数,通过求函数的最值的方法可求得它的最大值.
(2)沿![]() 将△
将△![]() 折起后,
折起后, ![]() 两两互相垂直,故可以
两两互相垂直,故可以![]() 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系![]() ,利用空间向量即可找到点N的位置,并求得
,利用空间向量即可找到点N的位置,并求得![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
试题解析:(1)解法1:在如图1所示的△![]() 中,设
中,设![]() ,则
,则![]() .
.
由![]() ,
, ![]() 知,△
知,△![]() 为等腰直角三角形,所以
为等腰直角三角形,所以![]() .
.
由折起前![]() 知,折起后(如图2),
知,折起后(如图2),![]() ,
, ![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() .又
.又![]() ,所以
,所以![]() .于是
.于是
![]()
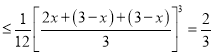 ,
,
当且仅当![]() ,即
,即![]() 时,等号成立,
时,等号成立,
故当![]() ,即
,即![]() 时,三棱锥
时,三棱锥![]() 的体积最大.
的体积最大.
解法2:同解法1,得![]() .
.
令![]() ,由
,由![]() ,且
,且![]() ,解得
,解得![]() .
.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以当![]() 时,
时, ![]() 取得最大值.
取得最大值.
故当![]() 时,三棱锥
时,三棱锥![]() 的体积最大.
的体积最大.
(2)以![]() 为原点,建立如图a所示的空间直角坐标系
为原点,建立如图a所示的空间直角坐标系![]() .
.
由(1)知,当三棱锥![]() 的体积最大时,
的体积最大时, ![]() ,
, ![]() .
.
于是可得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
且![]() .
.
设![]() ,则
,则![]() .因为
.因为![]() 等价于
等价于![]() ,即
,即
![]() ,故
,故![]() ,
, ![]() .
.
所以当![]() (即
(即![]() 是
是![]() 的靠近点
的靠近点![]() 的一个四等分点)时,
的一个四等分点)时, ![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,由
,由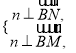 及
及![]() ,
,
得![]() 可取
可取![]() .
.
设![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ,则由
,则由![]() ,
, ![]() ,可得
,可得
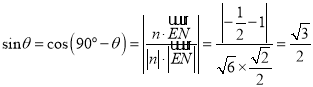 ,即
,即![]() .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目