题目内容
12.求函数y=5-x+$\sqrt{3x-1}$的值域.分析 带根号,可考虑换元去根号:可令$\sqrt{3x-1}=t$,t≥0,从而可解出x并带入原函数解析式,即可得到关于t的二次函数,从而可配方求该二次函数的值域即可.
解答 解:令$\sqrt{3x-1}=t$,t≥0,则x=$\frac{{t}^{2}+1}{3}$;
∴$y=5-\frac{{t}^{2}+1}{3}+t$=$-\frac{1}{3}(t-\frac{3}{2})^{2}+\frac{65}{12}$;
∵t≥0;
∴$-\frac{1}{3}(t-\frac{3}{2})^{2}+\frac{65}{12}≤\frac{65}{12}$;
∴该函数的值域为($-∞,\frac{65}{12}$].
点评 考查函数值域的概念,以及换元的方法去掉函数解析式中的根号,注意确定换元后新变量的范围,以及配方法求二次函数的值域.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
3.关于x的方程x2-(a2-1)x+a-2=0的一个根比1大,另一个根比1小,则有( )
| A. | -1<a<1 | B. | a<0或a>1 | C. | -2<a<1 | D. | a<-1或a>2 |
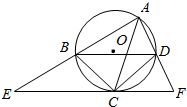 如图所示,四边形ABCD是⊙O的内接四边形,BD不经过点O,AC平分∠BAD,经过点C的直线分别交AB、AD的延长线于E、F,且CD2=AB•DF.
如图所示,四边形ABCD是⊙O的内接四边形,BD不经过点O,AC平分∠BAD,经过点C的直线分别交AB、AD的延长线于E、F,且CD2=AB•DF. 在正四棱柱ABCD-A1B1C1D1中,AB=2,E为AA1的中点,F为BB1的中点,面D1EB与底面ABCD所成角为arccos$\frac{\sqrt{6}}{3}$.
在正四棱柱ABCD-A1B1C1D1中,AB=2,E为AA1的中点,F为BB1的中点,面D1EB与底面ABCD所成角为arccos$\frac{\sqrt{6}}{3}$.