题目内容
(12分)已知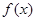 是定义在(0,+∞)上的增函数,且满足
是定义在(0,+∞)上的增函数,且满足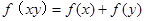 ,
, 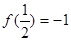
(1)求证: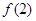 =1 (2) 求不等式
=1 (2) 求不等式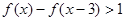 的解集.
的解集.
【答案】
(1)见解析;(2) {x/3<x<6}。
【解析】
试题分析:(1)由题意得f(1)=f(1×1)=f(1)+f(1)=2f(1) ∴f(1)=0,进一步得到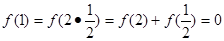 .
.
(2)不等式化为f(x)>f(x-3)+1
∵f(2)=1
∴f(x)>f(x-3)+f(2)=f(2x-6)
∵f(x)是(0,+∞)上的增函数
∴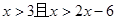 解得{x/3<x<6}
解得{x/3<x<6}
(1)【证明】 由题意得f(1)=f(1×1)=f(1)+f(1)=2f(1) ∴f(1)=0 3分
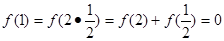 ∴
∴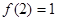 。。。6分
。。。6分
(2)【解】 不等式化为f(x)>f(x-3)+1
∵f(2)=1
∴f(x)>f(x-3)+f(2)=f(2x-6)
∵f(x)是(0,+∞)上的增函数
∴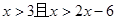 解得{x/3<x<6}
。。。。12分
解得{x/3<x<6}
。。。。12分
考点:本题主要是考查抽象函数单调性的运用。
点评:解决该试题的关键是利用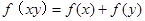 和
和 得到f(2)=1,进而变形得到不等式的解集。
得到f(2)=1,进而变形得到不等式的解集。

练习册系列答案
相关题目
 是定义在
是定义在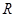 上的奇函数,当
上的奇函数,当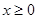 时,
时,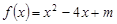 。
。
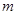 及
及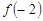 的值;
的值;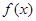 是定义在
是定义在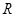 上的奇函数,且
上的奇函数,且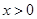 时,
时,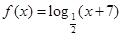 .
. 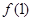 ,
,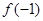
 ,求
,求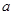 的取值范围
的取值范围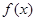 是定义在
是定义在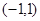 上的奇函数,且当
上的奇函数,且当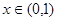 时,
时,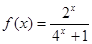 .
.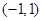 上的解析式;
上的解析式; 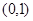 上是减函数;
上是减函数;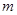 取何值时,
取何值时,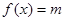 在
在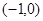 上有解.
上有解.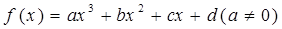 是定义在R上的函数, 且
是定义在R上的函数, 且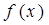 在(-1,0)和(4,5)上有相同的单调性,在(0,2)和(4,5)上
在(-1,0)和(4,5)上有相同的单调性,在(0,2)和(4,5)上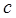 的值;
的值;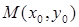 ,使得
,使得 的
的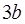 ?若存在,求出点
?若存在,求出点