题目内容
3.函数f(x)(x∈R)的图象如图所示,则g(x)=f(logax)(0<a<1)的单调递减区间为[$\sqrt{a}$,1]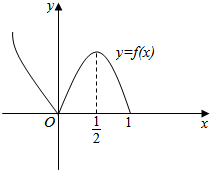
分析 可判断y=logax在(0,+∞)上是减函数,再由复合函数的单调性可知0≤logax≤$\frac{1}{2}$;从而解得.
解答 解:∵0<a<1,
∴y=logax在(0,+∞)上是减函数,
∴0≤logax≤$\frac{1}{2}$;
即$\sqrt{a}$≤x≤1;
即g(x)=f(logax)(0<a<1)的单调递减区间为[$\sqrt{a}$,1];
故答案为:[$\sqrt{a}$,1].
点评 本题考查了复合函数的单调性的应用及对数函数的应用,同时考查了学生读图的能力.

练习册系列答案
相关题目
18.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{a}$∥$\overrightarrow{b}$,|$\overrightarrow{a}$+$\overrightarrow{b}$|=3$\sqrt{5}$,则|$\overrightarrow{b}$|=( )
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 4$\sqrt{5}$ | D. | 2$\sqrt{5}$,或4$\sqrt{5}$ |