题目内容
【题目】如图所示,在棱长为2的正方体![]() 中,
中, ![]() 分别为
分别为![]() 和
和![]() 的中点.
的中点.
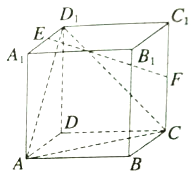
(1)求证: ![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ,若存在,求出
,若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1) 见解析(2) ![]() =
=![]()
【解析】试题分析:(1)分别以![]() 所在的直线为
所在的直线为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,面
,面![]() 的一个法向量是
的一个法向量是![]() ,由
,由![]() 即可证得;
即可证得;
(2)设点![]() 求解平面
求解平面![]() 的一个法向量为
的一个法向量为![]() ,平面
,平面![]() 的一个法向量
的一个法向量![]() 利用平面的法向量的夹角与二面角的大小之间的关系建立方程求解即可.
利用平面的法向量的夹角与二面角的大小之间的关系建立方程求解即可.
试题解析:
(1)证明:如图所示,分别以![]() 所在的直线为
所在的直线为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,由已知得
,由已知得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∵平面![]() 的一个法向量是
的一个法向量是![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,而
,而![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
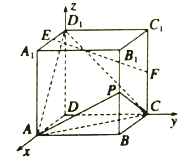
(2)解:设点![]() ,
,
平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则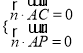 ,∵
,∵![]() ,
, ![]() ,
,
∴![]() ,取
,取![]() ,则
,则![]() ,
, ![]() ,∴
,∴![]() ,
,
平面![]() 的一个法向量
的一个法向量![]() ,
,
依题意知, ![]() 或
或![]() ,
,
∴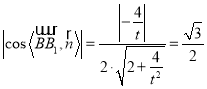 ,即
,即![]() ,解得
,解得![]() 或
或![]() (舍),
(舍),
∵![]() ,
,
∴在棱![]() 上存在一点
上存在一点![]() ,当
,当![]() 的长为
的长为![]() 时,二面角
时,二面角![]() 的大小为
的大小为![]() .
.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目

