题目内容
若函数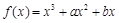
为奇函数，其图象的一条切线方程为
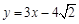，则b的值为 ．
-3
解析试题分析：由奇函数的定义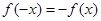
，易得
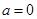，对函数求导可得：
，可设切点
，则有
，可解得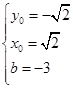
.
考点：1.函数的性质;2.曲线的切线
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
学练快车道口算心算速算天天练系列答案题目内容
若函数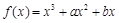为奇函数，其图象的一条切线方程为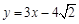，则b的值为 ．
-3
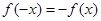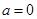解析试题分析：由奇函数的定义，易得，对函数求导可得：，可设切点，则有，可解得.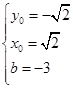
考点：1.函数的性质;2.曲线的切线
学练快车道口算心算速算天天练系列答案
，若
，则
；
左侧的图形的面积为
，则
的图像与直线
轴围成的图形面积为______.
则
的值为.
在区间
上取得最小值4，则
___________．
= .
和
，使得函数
和
对其定义域上的任意实数
分别满足：
和
，则称直线
为
和函数
，那么函数