题目内容
(1)求函数f(x)=2x3-9x2+12x-3的单调递减区间；(2)求函数y=x3-2x2+x的单调区间.
解析：(1)f′(x)=6x2-18x+12=6(x-1)(x-2).
令6(x-1)(x-2)＜0，解得1＜x＜2.
所以函数f(x)的单调递减区间为(1,2).
(2)y′=3x2-4x+1.
令3x2-4x+1＞0,解得x＞1或x＜
.
因此y=x3-2x2+x的单调递增区间为(1，+∞),(-∞,
).
再令3x2-4x+1＜0,解得
＜x＜1.因此y=x3-2x2+x的单调递减区间为(
，1).
练习册系列答案
考前必练系列答案
相关题目
+lg
,
×
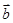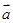="(2cosx,1)," 
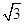sin2x+m)．
]时,ô f(x)ô <4恒成立，求实数m的取值范围．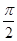
)的部分图象．
＝
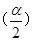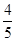，0<α<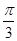
，求cosα的值．
是定义在(－1,1)上的奇函数，且f(
)＝
.