题目内容
不等式(x+2)(x-1)2(3-x)3≥0的解集为( )
分析:利用穿根法“奇”过“偶”不过,即可求得答案.
解答:解:∵(x+2)(x-1)2(3-x)3≥0,
∴(x+2)(x-1)2(x-3)3≤0,
由穿根法“奇”过“偶”不过,
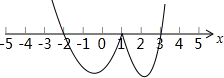
得:-2≤x≤3.
∴原不等式的解集为{x|-2≤x≤3}.
故选C.
∴(x+2)(x-1)2(x-3)3≤0,
由穿根法“奇”过“偶”不过,

得:-2≤x≤3.
∴原不等式的解集为{x|-2≤x≤3}.
故选C.
点评:本题考查高次不等式的解法,考查穿根法应用,将不等式(x+2)(x-1)2(3-x)3≥0转化为不等式(x+2)(x-1)2(x-3)3≤0是关键,属于中档题.

练习册系列答案
相关题目