题目内容
(本小题满分15分)
在平面直角坐标系中,已知点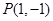 ,过点
,过点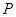 作抛物线
作抛物线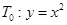 的切线,其切点分别为
的切线,其切点分别为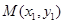 、
、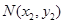 (其中
(其中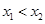 ).
).
(1)求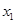 与
与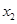 的值;
的值;
(2)若以点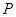 为圆心的圆
为圆心的圆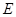 与直线
与直线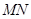 相切,求圆
相切,求圆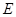 的面积;
的面积;
(3)过原点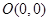 作圆
作圆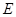 的两条互相垂直的弦
的两条互相垂直的弦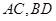 ,求四边形
,求四边形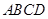 面积的最大值.
面积的最大值.
【答案】
解:(Ⅰ)由 可得,
可得, .……1分
.……1分
∵直线 与曲线
与曲线 相切,且过点
相切,且过点 ,∴
,∴ ,即
,即 ,
,
∴ ,或
,或 , ……3分
, ……3分
同理可得: ,或
,或 ……4分
……4分
∵ ,∴
,∴ ,
, . ……5分
. ……5分
(Ⅱ)由(Ⅰ)知, ,
, ,则直线
,则直线 的斜率
的斜率
 ,……6分
,……6分
∴直线 的方程为:
的方程为: ,又
,又 ,
,
∴ ,即
,即 .
……7分
.
……7分
∵点 到直线
到直线 的距离即为圆
的距离即为圆 的半径,即
的半径,即 , ……8分
, ……8分
故圆 的面积为
的面积为 .……9分
.……9分
(Ⅲ)四边形 的面积为
的面积为
不妨设圆心 到直线
到直线 的距离为
的距离为 ,垂足为
,垂足为 ;圆心
;圆心 到直线
到直线 的距离为
的距离为 ,垂足为
,垂足为 ;则
;则 ……10分
……10分
由于四边形 为矩形.且
为矩形.且 ……11分
……11分
所以 ,由基本不等式
,由基本不等式 可得
可得
 ,
,
当且仅当 时等号成立. ……15分
时等号成立. ……15分
【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 的单调区间;
的单调区间; ,试分别解答以下两小题.
,试分别解答以下两小题. 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 是两个不相等的正数,且
是两个不相等的正数,且 ,求证:
,求证: .
. 、
、 分别为椭圆
分别为椭圆 :
: 的
的  :
: 的焦点,
的焦点, 是
是 。
。 :
: ,过点P的动直线
,过点P的动直线 与圆
与圆 ,
, (
( 且
且 )。求证:点Q总在某定直线上。
)。求证:点Q总在某定直线上。
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,过
,过 与椭圆相交于A、B两点。
与椭圆相交于A、B两点。 ,且
,且 ,求椭圆的离心率;
,求椭圆的离心率; 求
求 的最大值和最小值。
的最大值和最小值。
 在定义域内存在区间
在定义域内存在区间 ,满足
,满足 是否为“优美函数”?若是,求出
是否为“优美函数”?若是,求出 ;若不是,说明理由;
;若不是,说明理由; 为“优美函数”,求实数
为“优美函数”,求实数 的取值范围.
的取值范围.