题目内容
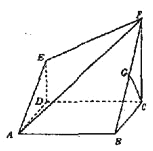
【题目】设函数![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交函数
交函数![]() 图象于点
图象于点![]() ,以
,以![]() 为切点作函数
为切点作函数![]() 图象的切线交
图象的切线交![]() 轴于点
轴于点![]() ,再过
,再过![]() 作
作![]() 轴的垂线
轴的垂线![]() 交函数
交函数![]() 图象于点
图象于点![]() ,
,![]() ,以此类推得点
,以此类推得点![]() ,记
,记![]() 的横坐标为
的横坐标为![]() ,
,![]() .
.
(1)证明数列![]() 为等比数列并求出通项公式;
为等比数列并求出通项公式;
(2)设直线![]() 与函数
与函数![]() 的图象相交于点
的图象相交于点![]() ,记
,记![]() (其中
(其中![]() 为坐标原点),求数列
为坐标原点),求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)证明见解析,![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据导数的几何意义可求得以点![]() 为切点的切线方程,代入
为切点的切线方程,代入![]() 可求得
可求得![]() ,由此可得数列
,由此可得数列![]() 为等比数列,根据等比数列通项公式求得结果;
为等比数列,根据等比数列通项公式求得结果;
(2)根据向量数量积的坐标运算可求得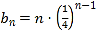 ,利用错位相减法可求得结果.
,利用错位相减法可求得结果.
(1)证明:![]() 函数
函数![]() ,
,![]() ,
,
![]() 以点
以点![]() 为切点的切线方程为:
为切点的切线方程为:![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,
,
又![]() ,
,![]() 数列
数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列,
为公比的等比数列,![]() .
.
(2)解:由题意得: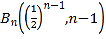 ,
,
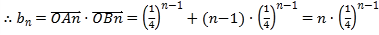 ,
,
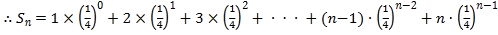 …①,
…①,
则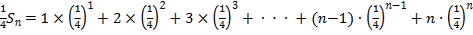 …②,
…②,
①![]() ②得:
②得:
![]() ,
,
![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】据《人民网》报道,美国国家航空航天局(NASA)发文称,相比20年前世界变得更绿色了,卫星资料显示中国和印度的行动主导了地球变绿.据统计,中国新增绿化面积的![]() 来自于植树造林,下表是中国十个地区在去年植树造林的相关数据.(造林总面积为人工造林、飞播造林、新封山育林、退化林修复、人工更新的面积之和)
来自于植树造林,下表是中国十个地区在去年植树造林的相关数据.(造林总面积为人工造林、飞播造林、新封山育林、退化林修复、人工更新的面积之和)
单位:公顷
地区 | 造林总面积 | 造林方式 | ||||
人工造林 | 飞播造林 | 新封山育林 | 退化林修复 | 人工更新 | ||
内蒙 | 618484 | 311052 | 74094 | 136006 | 90382 | 6950 |
河北 | 583361 | 345625 | 33333 | 13507 | 65653 | 3643 |
河南 | 149002 | 97647 | 13429 | 22417 | 15376 | 133 |
重庆 | 226333 | 100600 | 62400 | 63333 | ||
陕西 | 297642 | 184108 | 33602 | 63865 | 16067 | |
甘肃 | 325580 | 260144 | 57438 | 7998 | ||
新疆 | 263903 | 118105 | 6264 | 126647 | 10796 | 2091 |
青海 | 178414 | 16051 | 159734 | 2629 | ||
宁夏 | 91531 | 58960 | 22938 | 8298 | 1335 | |
北京 | 19064 | 10012 | 4000 | 3999 | 1053 | |
(1)请根据上述数据分别写出在这十个地区中人工造林面积与造林总面积的比值最大和最小的地区;
(2)在这十个地区中,任选一个地区,求该地区新封山育林面积占造林总面积的比值超过![]() 的概率;
的概率;
(3)在这十个地区中,从退化林修复面积超过一万公顷的地区中,任选两个地区,记X为这两个地区中退化林修复面积超过六万公顷的地区的个数,求X的分布列及数学期望.