题目内容
对于函数f(x)=
,下列结论正确的是
①f(x)在(-∞,+∞)上不是单调函数
②?m∈(0,1),使得方程f(x)=m有两个不等的实数解;
③?k∈(1,+∞),使得函数g(x)=f(x)-kx在R上有三个零点;
④?x1,x2∈R,若x1≠x2,则f(x1)≠f(x2).
| x | 1+|x| |
④
④
.①f(x)在(-∞,+∞)上不是单调函数
②?m∈(0,1),使得方程f(x)=m有两个不等的实数解;
③?k∈(1,+∞),使得函数g(x)=f(x)-kx在R上有三个零点;
④?x1,x2∈R,若x1≠x2,则f(x1)≠f(x2).
分析:①判断函数是奇函数,再用导数法确定函数的单调性即可;
②利用函数在实数集R上具有单调性,即可得到结论;
③0是方程f(x)-kx=0的一个根<而当x>0,k>1时,方程
-kx=0无解,即函数g(x)无零点,同理x<0时,亦无解,故③不正确;
④由②的单调性即可判断出
②利用函数在实数集R上具有单调性,即可得到结论;
③0是方程f(x)-kx=0的一个根<而当x>0,k>1时,方程
| x |
| 1+x |
④由②的单调性即可判断出
解答:解:函数f(x)=
的定义域为实数集R,图象如图所示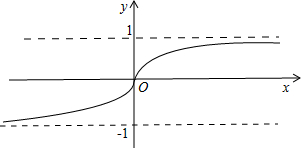
①?x∈R,f(-x)+f(x)=
+
=0
函数是实数集R上的奇函数,其图象关于原点对称
∵x>0时,f(x)=
,∴f′(x)=
>0
∴函数是实数集R上的单调增函数,故①不正确;
②由①知,m∈(0,1),方程f(x)=m有唯一实数解,故②不正确;
③∵g(0)=f(0)-0=0,∴x=0是函数g(x)的一个零点;
当x>0时,若?k∈(1,+∞),使得函数g(x)=f(x)-kx在区间(0,+∞)上有零点,则方程
-kx=0必有解,此方程化为kx=1-k,
∵x=
<0,∴此方程无解,∴不存在k∈(1,+∞),使得函数g(x)=f(x)-kx在区间(0,+∞)上有零点;
同理不存在k∈(1,+∞),使得函数g(x)=f(x)-kx在区间(-∞,0)上有零点,故③不正确;
④由②可知:函数f(x)=
,在实数集R上单调递增,因此?x1,x2∈R,若x1≠x2,则f(x1)≠f(x2),故④正确.
综上可知:只有④正确.
故答案为:④.
| x |
| 1+|x| |
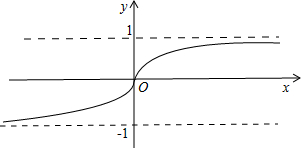
①?x∈R,f(-x)+f(x)=
| -x |
| 1+|-x| |
| x |
| 1+|x| |
函数是实数集R上的奇函数,其图象关于原点对称
∵x>0时,f(x)=
| x |
| 1+x |
| 1 |
| (1+x)2 |
∴函数是实数集R上的单调增函数,故①不正确;
②由①知,m∈(0,1),方程f(x)=m有唯一实数解,故②不正确;
③∵g(0)=f(0)-0=0,∴x=0是函数g(x)的一个零点;
当x>0时,若?k∈(1,+∞),使得函数g(x)=f(x)-kx在区间(0,+∞)上有零点,则方程
| x |
| 1+x |
∵x=
| 1-k |
| k |
同理不存在k∈(1,+∞),使得函数g(x)=f(x)-kx在区间(-∞,0)上有零点,故③不正确;
④由②可知:函数f(x)=
| x |
| 1+|x| |
综上可知:只有④正确.
故答案为:④.
点评:本题考查函数的性质,考查学生分析解决问题的能力,由已知函数得出其奇偶性和单调性及画出图形是解题的关键.

练习册系列答案
相关题目