题目内容
已知数列{an}是由正数构成的数列,a1=3,且满足lgan=lgan-1+lgc,其中n是大于1的整数,c是正数.
(1)求数列{an}的通项公式及前n和Sn;
(2)求
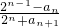 的值.
的值.
解:(1)由已知得an=c•an-1,
∴{an}是以a1=3,公比为c的等比数列,则an=3•cn-1.
∴Sn=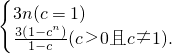
(2)
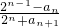 =
=
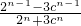 .
.
①当c=2时,原式=- ;
;
②当c>2时,原式=
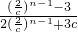 =-
=- ;
;
③当0<c<2时,原式=
 =
= .
.
分析:(1)由已知得an=3•cn-1.由此可知Sn=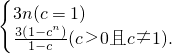
(2)
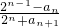 =
=
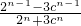 .再由c的取值范围分别讨论
.再由c的取值范围分别讨论
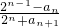 的值.
的值.
点评:求数列极限时要注意分类讨论思想的应用.
∴{an}是以a1=3,公比为c的等比数列,则an=3•cn-1.
∴Sn=
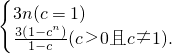
(2)

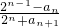 =
=
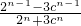 .
.①当c=2时,原式=-
 ;
;②当c>2时,原式=

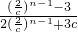 =-
=- ;
;③当0<c<2时,原式=

 =
= .
.分析:(1)由已知得an=3•cn-1.由此可知Sn=
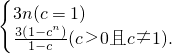
(2)

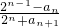 =
=
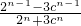 .再由c的取值范围分别讨论
.再由c的取值范围分别讨论
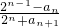 的值.
的值.点评:求数列极限时要注意分类讨论思想的应用.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目