题目内容
设对任意实数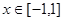 ,不等式
,不等式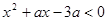 恒成立,则实数
恒成立,则实数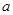 的取值范围是
的取值范围是
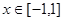 ,不等式
,不等式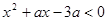 恒成立,则实数
恒成立,则实数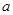 的取值范围是
的取值范围是A.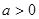 | B.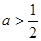 | C.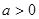 或 或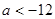 | D.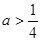 |
B
记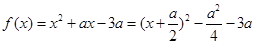 。当
。当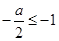 即
即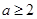 时,
时,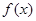 在区间
在区间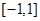 上单调递增,所以此时
上单调递增,所以此时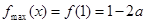 ,从而有
,从而有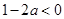 ,解得
,解得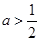 。所以此时
。所以此时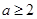 ;
;
当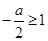 即
即 时,
时,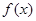 在区间
在区间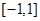 上单调递减,所以此时
上单调递减,所以此时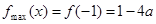 ,从而有
,从而有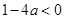 ,解得
,解得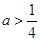 ,与
,与 矛盾,此时无解;
矛盾,此时无解;
当 时,
时, ,所以此时
,所以此时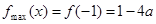 ,从而有
,从而有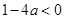 ,解得
,解得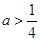 ,与
,与 矛盾,此时也无解;
矛盾,此时也无解;
当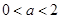 时,
时, ,所以此时
,所以此时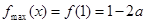 ,从而有
,从而有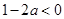 ,解得
,解得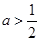 。所以此时
。所以此时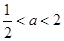 。
。
综上可得,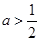 ,故选B
,故选B
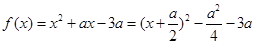 。当
。当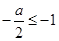 即
即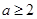 时,
时,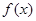 在区间
在区间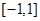 上单调递增,所以此时
上单调递增,所以此时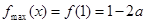 ,从而有
,从而有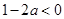 ,解得
,解得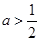 。所以此时
。所以此时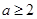 ;
;当
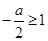 即
即 时,
时,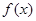 在区间
在区间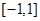 上单调递减,所以此时
上单调递减,所以此时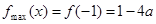 ,从而有
,从而有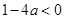 ,解得
,解得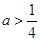 ,与
,与 矛盾,此时无解;
矛盾,此时无解;当
 时,
时, ,所以此时
,所以此时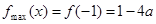 ,从而有
,从而有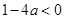 ,解得
,解得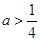 ,与
,与 矛盾,此时也无解;
矛盾,此时也无解;当
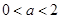 时,
时, ,所以此时
,所以此时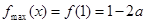 ,从而有
,从而有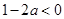 ,解得
,解得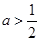 。所以此时
。所以此时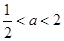 。
。综上可得,
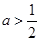 ,故选B
,故选B
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在[-1,1]上是增函数,且
在[-1,1]上是增函数,且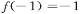 ,若函数
,若函数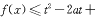 1对所有
1对所有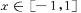 都成立,则当
都成立,则当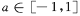 时t的取值范围是____
时t的取值范围是____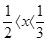 },则b-a的值等于
},则b-a的值等于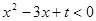 的解集为
的解集为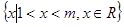
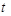 、
、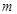 的值;
的值;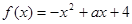 在区间
在区间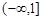 上递增,求关于
上递增,求关于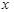 的不等式
的不等式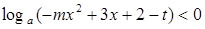 的解集。
的解集。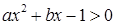 的解集是
的解集是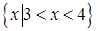 ,则
,则 ;
;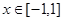 ,不等式
,不等式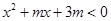 恒成立,则实数
恒成立,则实数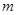 的取值范围是 .
的取值范围是 . 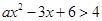 的解集为
的解集为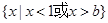 .
.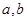 ; (2)解关于
; (2)解关于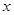 的不等式
的不等式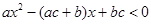 .
. 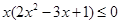 的解集为_____________.
的解集为_____________.