题目内容
设奇函数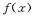
在[-1,1]上是增函数，且
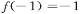，若函数
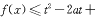1对所有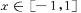
都成立，则当
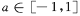时t的取值范围是____
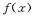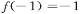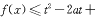在[-1,1]上是增函数，且，若函数1对所有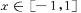都成立，则当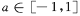时t的取值范围是____t≤－2或t=0或t≥2
若函数f（x）≤t2-2at+1对所有的x∈[-1，1]都成立，由已知易得f（x）的最大值是1，
∴1≤t2-2at+1?2at-t2≤0，
设g（a）=2at-t2（-1≤a≤1），
欲使2at-t2≤0恒成立，则
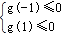
?t≥2@t=0@t≤-2．
答案：t≤-2或t=0或t≥2
∴1≤t2-2at+1?2at-t2≤0，
设g（a）=2at-t2（-1≤a≤1），
欲使2at-t2≤0恒成立，则
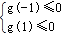
?t≥2@t=0@t≤-2．
答案：t≤-2或t=0或t≥2
练习册系列答案
一本好题口算题卡系列答案
相关题目
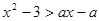对一切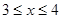
恒成立，则实数
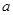的取值范围是______________.
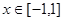，不等式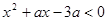
恒成立，则实数
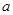的取值范围是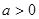
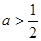
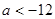
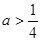
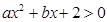的解集为
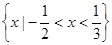，则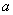
+
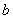的值_______.
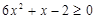的解集是（ ）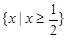
，
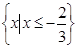
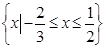
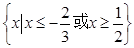
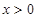，则实数
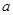的取值范围是 
、
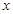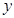满足
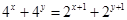，则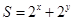
的取值范围是 ▲ ．
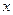，使得
成立，则
的取值范围是___▲___．