题目内容
若对任意实数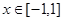 ,不等式
,不等式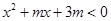 恒成立,则实数
恒成立,则实数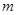 的取值范围是 .
的取值范围是 .
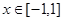 ,不等式
,不等式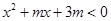 恒成立,则实数
恒成立,则实数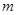 的取值范围是 .
的取值范围是 . 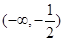
本题考查恒成立问题的解法
设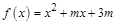 ,则
,则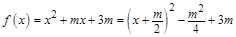
当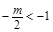 时,即
时,即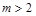 时,
时,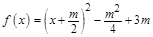 在区间
在区间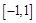 上递增,则
上递增,则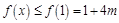 ,由题意有
,由题意有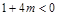 ,解得
,解得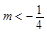 .因
.因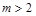 ,则
,则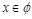 .
.
当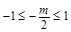 时,即
时,即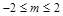 时,等式
时,等式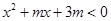 恒成立,则
恒成立,则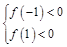
即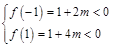 ,解得
,解得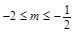 .
.
当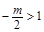 时,即
时,即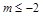 时,
时,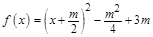 在区间
在区间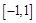 上递减,由不等式
上递减,由不等式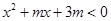 恒成立,则
恒成立,则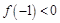 ,即
,即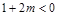 ,解得
,解得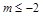 .
.
综上可得实数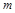 的取值范围为
的取值范围为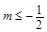
.
设
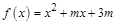 ,则
,则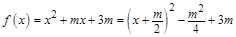
当
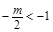 时,即
时,即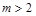 时,
时,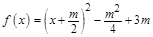 在区间
在区间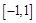 上递增,则
上递增,则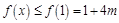 ,由题意有
,由题意有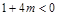 ,解得
,解得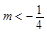 .因
.因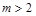 ,则
,则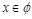 .
.当
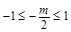 时,即
时,即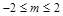 时,等式
时,等式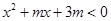 恒成立,则
恒成立,则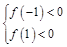
即
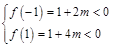 ,解得
,解得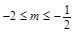 .
.当
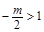 时,即
时,即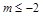 时,
时,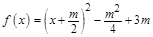 在区间
在区间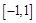 上递减,由不等式
上递减,由不等式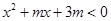 恒成立,则
恒成立,则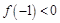 ,即
,即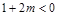 ,解得
,解得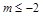 .
.综上可得实数
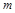 的取值范围为
的取值范围为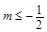
.

练习册系列答案
相关题目
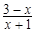 ≤0的解集是
≤0的解集是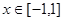 ,不等式
,不等式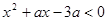 恒成立,则实数
恒成立,则实数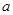 的取值范围是
的取值范围是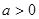
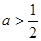
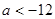
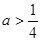
 的解集为:
的解集为: 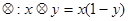 ,若不等式
,若不等式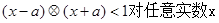 成立,则实数a的取值范围是
成立,则实数a的取值范围是



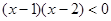 的解集为 ★ .
的解集为 ★ .
 的不等式
的不等式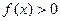 的解集是(-1,3),求实数
的解集是(-1,3),求实数  的值。
的值。 的不等式
的不等式
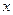 ,使得
,使得 成立,则
成立,则 的取值范围是___▲___.
的取值范围是___▲___.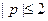 的不等式
的不等式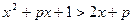 恒成立,则实数x的取值范围是 .
恒成立,则实数x的取值范围是 .