证明一个角的平分线的平行射影不一定是该角平行射影的角平分线.图3-1-5 题目和参考答案——青夏教育精英家教网——

题目内容

证明一个角的平分线的平行射影不一定是该角平行射影的角平分线.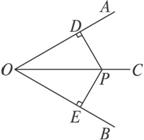

图3-1-5

证明:设OC为∠AOB的平分线,在OC上任取一点P,作PD⊥OA于D,PE⊥OB于E.

显然必存在一平面α∥PD而不平行于PE,将该角向平面α作正射影,

则PD=P′D′,PE＞P′E′.

∵PD=PE,

∴P′D′＞P′E′,即P′不在∠A′O′B′的角平分线上.

练习册系列答案

新导航全程测试卷系列答案

新编初中总复习系列答案

校园英语英语大课堂系列答案

小状元金考卷单元考点梳理系列答案

小学总复习冲刺卷系列答案

小学总复习教程系列答案

通城学典小学总复习系列答案

小学综合能力测评同步训练系列答案

名师伴你总复习系列答案

步步通优系列答案

相关题目

（1）若椭圆的方程是：

=1（a＞b＞0），它的左、右焦点依次为F₁、F₂，P是椭圆上异于长轴端点的任意一点．在此条件下我们可以提出这样一个问题：“设△PF₁F₂的过P角的外角平分线为l，自焦点F₂引l的垂线，垂足为Q，试求Q点的轨迹方程？”
对该问题某同学给出了一个正确的求解，但部分解答过程因作业本受潮模糊了，我们在

这些模糊地方划了线，请你将它补充完整．
解：延长F₂Q 交F₁P的延长线于E，据题意，
E与F₂关于l对称，所以|PE|=|PF₂|．
所以|EF₁|=|PF₁|+|PE|=|PF₁|+|PF₂|=

，
在△EF₁F₂中，显然OQ是平行于EF₁的中位线，
所以|OQ|=

，
注意到P是椭圆上异于长轴端点的点，所以Q点的轨迹是

，
其方程是：

．
（2）如图2，双曲线的方程是：

=1（a，b＞0），它的左、右焦点依次为F₁、F₂，P是双曲线上异于实轴端点的任意一点．请你试着提出与（1）类似的问题，并加以证明．

（2013•山东）椭圆C：

=1(a＞0，b＞0)的左右焦点分别是F₁，F₂，离心率为

，过F₁且垂直于x轴的直线被椭圆C截得的线段长为1．
（1）求椭圆C的方程；
（2）点P是椭圆C上除长轴端点外的任一点，连接PF₁，PF₂，设∠F₁PF₂的角平分线PM交C的长轴于点M（m，0），求m的取值范围；
（3）在（2）的条件下，过点P作斜率为k的直线l，使得l与椭圆C有且只有一个公共点，设直线PF₁，PF₂的斜率分别为k₁，k₂，若k≠0，试证明

为定值，并求出这个定值．

椭圆C：的左、右焦点分别是F₁．F₂，离心率为过F，且垂直于x轴的直线被椭圆C截得的线段长为l．

(Ⅰ)求椭圆C的方程；

(Ⅱ)点P是椭圆C上除长轴端点外的任一点，连接PF₁，PF₂，设∠F₁PF₂的角平分线PM交C的长轴于点M(m，0)，求m的取值范围；

(Ⅲ)在(Ⅱ)的条件下，过点p作斜率为k的直线l，使得l与椭圆C有且只有一个公共点．

设直线PF₁，PF₂的斜率分别为k₁，k₂，若k≠0，试证明为定值，并求出这个定值．

椭圆：的左、右焦点分别是，离心率为，过且垂直于轴的直线被椭圆截得的线段长为。

（Ⅰ）求椭圆的方程；

（Ⅱ）点是椭圆上除长轴端点外的任一点，连接，设的角平分线交的长轴于点，求的取值范围；

（Ⅲ）在（Ⅱ）的条件下，过点作斜率为的直线,使与椭圆有且只有一个公共点，设直线的斜率分别为。若，试证明为定值，并求出这个定值。