题目内容
已知：如图，AB是⊙O的弦，点C在  |
| AB |
（1）若∠OAB=35°，求∠AOB的度数；
（2）过点C作CD∥AB，若CD是⊙O的切线，求证：点C是
|
| AB |
分析：（1）根据等边对等角和三角形的内角和定理进行计算即可求∠AOB的度数；
（2）连接OC，根据切线的性质、平行线的性质和垂径定理进行证明．
（2）连接OC，根据切线的性质、平行线的性质和垂径定理进行证明．
解答：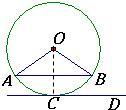
解：（1）∵OA=OB，∠OAB=35°，
∴∠OBA=∠OAB=35°．
∴∠AOB=110°．
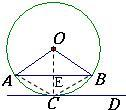
（2）证明：连接OC，
∵CD为⊙O的切线，
∴OC⊥CD又AB∥CD，
∴OC⊥AB．
∴
=
．
即C是
的中点．
解：（1）∵OA=OB，∠OAB=35°，∴∠OBA=∠OAB=35°．
∴∠AOB=110°．
（2）证明：连接OC，
∵CD为⊙O的切线，
∴OC⊥CD又AB∥CD，
∴OC⊥AB．
∴
|
| AC |
|
| BC |
即C是
|
| AB |
点评：本题主要考查了圆的切线的性质定理，属于基础题，此题综合运用了切线的性质、平行线的性质和垂径定理进行证明．
练习册系列答案
相关题目
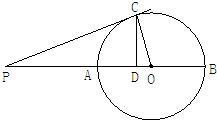已知：如图，AB是⊙O的直径，点C是⊙O上一点，CD⊥AB，垂足为D，点P在BA的延长线上，且PC是圆O的切线．
【选修4-1：几何证明选讲】
已知：如图，AB是圆C：x2+y2+4x-12y+24=0的弦，且过点P（0，5）．